Breking treedt op wanneer een lichtstraal van het ene medium naar het andere overgaat (bijv. van lucht naar glas). De oorzaak van breking is een toename of afname in de lichtsnelheid (v). Hoewel in de lege ruimte de lichtsnelheid gelijk is aan c, is deze lager in andere media. De factor waardoor c gedeeld wordt, heet de brekingsindex (n) van het materiaal:
$$n = \frac{c}{v}.$$
Voorbeeld: In een stuk glas is de lichtsnelheid $v \approx 2 \cdot 10^8 \; \text{m/s}$. Wat is de brekingsindex?
Dit is anderhalf keer zo langzaam is als de snelheid in de lege ruimte, $c = 3 \cdot 10^8 \; \text{m/s}$. De brekingsindex van het glas is dus gelijk aan 1,5.
Als licht van het ene medium naar het andere overgaat,
- breekt het naar de normaal toe als de brekingsindex toeneemt (ofwel het licht vertraagt);
- breekt het van de normaal af als de brekingsindex afneemt (ofwel het licht versnelt).
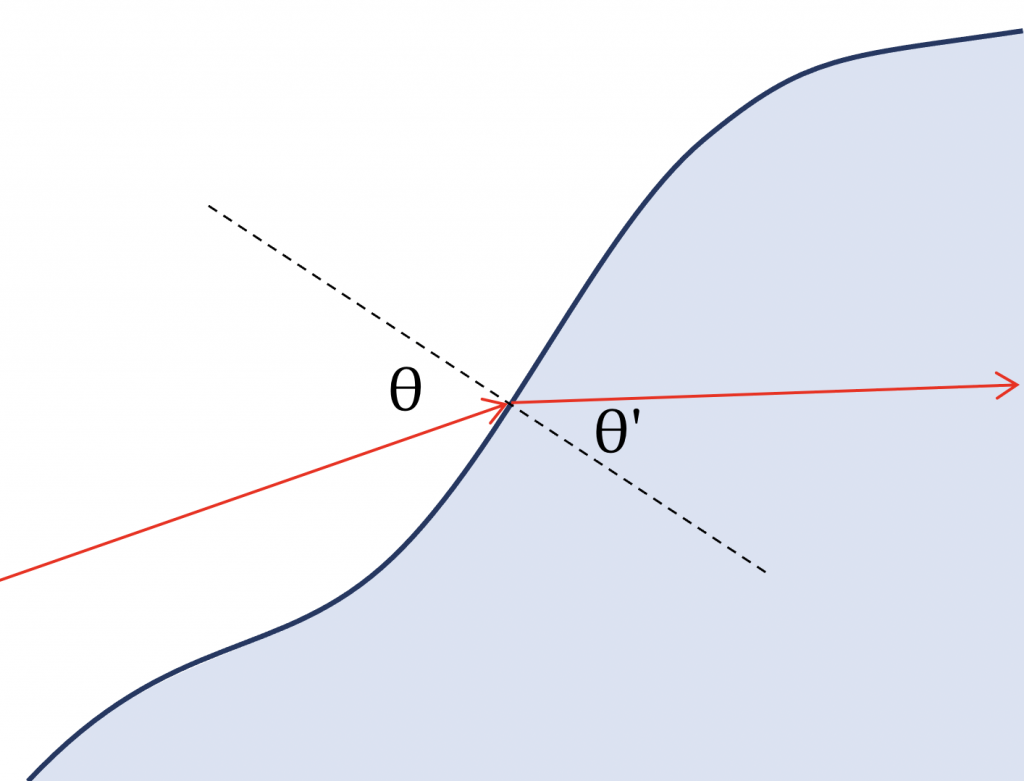
De wet van Snellius geeft de details:
$$n’\cdot \sin\theta’ = n \cdot \sin\theta.$$
Hierbij is:
- θ de invalshoek, tussen de invallende lichtstraal en de normaal;
- θ’ de brekingshoek, tussen de gebroken lichtstraal en de normaal;
- n, n’ de brekingsindex van het medium dat het licht verlaat / betreedt.
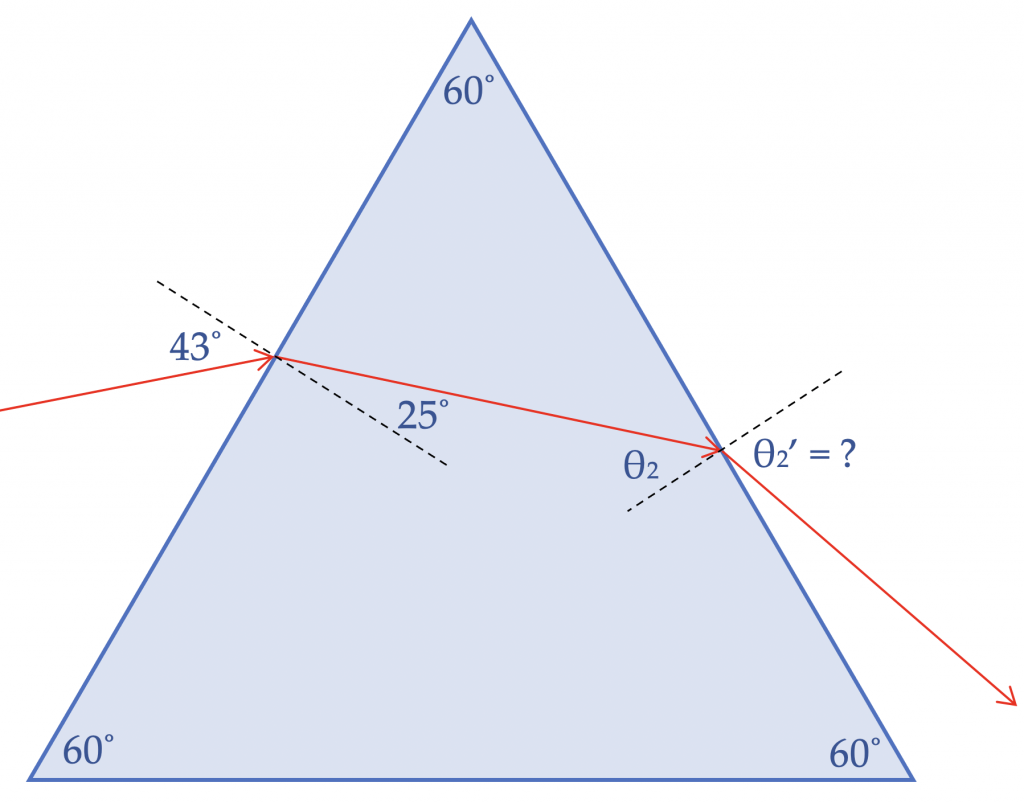
Voorbeeld: Het volgende diagram laat zien hoe een lichtstraal door een glazen prisma gaat. Bepaal (a) de brekingsindex van het glas; (b) de hoek waaronder het licht het prisma verlaat. De brekingsindex van lucht nlucht ≈ 1,00.
(a) Gebruik de informatie aan de linkerkant.
$$n’= \frac{n \cdot \sin\theta_1}{\sin \theta_1′} = \frac{1{,}00 \cdot \sin 43^\circ}{\sin 25^\circ} = 1{,}61$$
(b) Men moet eerst de invalshoek bepalen voor de rechterkant. De driehoek gevormd door de lichtstraal en de bovenkant van het prisma heeft een hoek van 60˚, een hoek van 90 – 25 = 65˚, en dus ook een hoek van 55˚ (het totaal is immers 180˚). Dit geeft een invalshoek van 90 – 55 = 35˚.
Nu lossen we op:
$$\sin\theta_2’= \frac{n \cdot \sin\theta_2}{n’} = \frac{1{,}61 \cdot \sin 35^\circ}{1{,}00} = 0{,}92;\ \ \theta_2′ = 68^\circ.$$
