Wanneer een blok hout onder water gehouden wordt, is de drijfkracht groter dan de zwaartekracht. De resultante kracht zal daardoor het blok omhoogduwen. Hoe verder het blok boven water uitsteekt, des te zwakker de drijfkracht wordt. Uiteindelijk wordt een evenwicht bereikt waarin de drijfkracht en zwaartekracht gelijk zijn: het blok drijft.
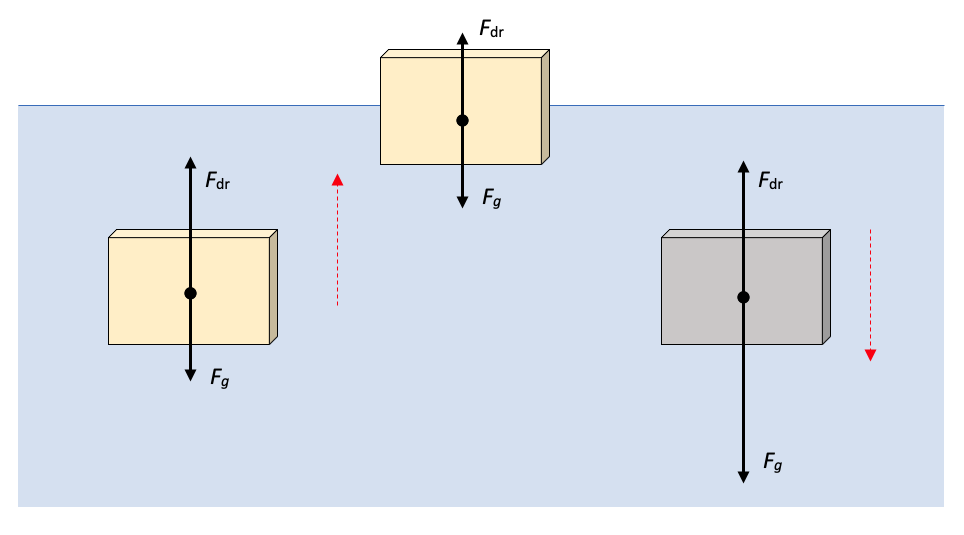
Midden: Het blok steekt boven het oppervlak uit; het verplaatst minder vloeistof, dus is er minder drijfkracht. Wanneer Fdr = Fg, drijft het blok.
Rechts: Een even groot metalen blok. Evenveel water wordt verplaatst, dus de drijfkracht is hetzelfde als bij het houten blok. Echter, door de hogere dichtheid van het metaal is de zwaartekracht groter. Fdr < Fg en het blok zinkt omlaag.
Een voorwerp drijft als de drijfkracht en de zwaartekracht elkaar opheffen. In dat geval wordt het voorwerp dus “gedragen” door de vloeistof. Een voorwerp zinkt als de drijfkracht te klein is om de zwaartekracht op te heffen, zelfs als het voorwerp geheel ondergedompeld is. Uit het beginsel van Archimedes kan men de volgende regels afleiden.
Om te bepalen of een voorwerp zal drijven of zinken: Vergelijk de dichtheden van het voorwerp en de vloeistof.
- Als $ \rho_{\text{voorwerp}} = \rho_{\text{vloeistof}}\,$, zal het voorwerp blijven zweven.
- Als $ \rho_{\text{voorwerp}} < \rho_{\text{vloeistof}}\,$, zal het voorwerp gaan drijven.
- Als $ \rho_{\text{voorwerp}} > \rho_{\text{vloeistof}}\,$, zal het voorwerp zinken.
Om te bepalen hoe diep een voorwerp zal drijven: Als een voorwerp drijft, is het maar gedeeltelijk ondergedompeld: Vverplaatst < Vvoorwerp. In evenwicht geldt:
$$V_{\text{verplaatst}} =V_{\text{voorwerp}} \cdot \frac{\rho_{\text{voorwerp}}}{\rho_{\text{vloeistof}}}.$$
Voorbeeld: IJs heeft een dichtheid van 920 kg/m3. Welk deel van een drijvend ijsklontje of van een drijvende ijsberg zal boven water uitsteken?
$$V_{\text{verplaatst}} = V_{\text{voorwerp}} \cdot \frac{920 \; \text{kg/m}^3}{1000 \; \text{kg/m}^3} = 0{,}92\; V_{\text{voorwerp}};$$
dus bevindt 92% van het ijs zich onder water; 8% ervan steekt boven water uit.
