Een gemengde schakeling is geen serieschakeling, en ook geen parallelschakeling. In dit geval is er geen eenvoudige formule te geven voor de vervangingsweerstand. Om een gemengde schakeling te analyseren moet men zoeken naar een deelschakeling die wél serie- of parallelschakeling is. Die vervangt men dan door een enkele weerstand (de vervangingsweerstand van de deelschakeling), zodat een eenvoudigere schakeling ontstaat.
In de rest van deze paragraaf bepalen wij de vervangingsweerstand van de volgende gemengde schakelingen.
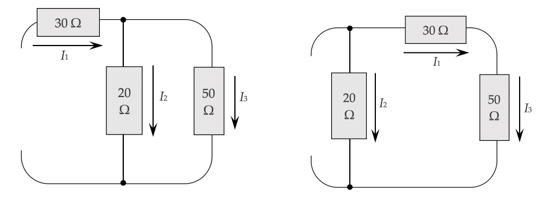
Voorbeeld 1

In deze schakeling gaat eerst alle stroom door de eerste weerstand; pas daarna vertakt de stroom zich. Dit is geen serieschakeling, omdat de stroom zich vertakt; maar ook geen parallelschakeling, omdat de stroom zich niet meteen vertakt.
Echter, de weerstanden van 20 Ω en 50 Ω vormen wel een parallelschakeling. Daarom analyseren wij deze combinatie eerst. Hun vervangingsweerstand is
$$\frac{1}{R_{23}}=\frac{1}{20} + \frac{1}{50}; \; R_{23} = 14 \;\Omega.$$
(De notatie R23 betekent: vervangingsweerstand van R2 en R3.)
Nu tekenen wij de schakeling nogmaals, maar vervangen de parallel geschakelde weerstanden door een enkele weerstand van 14 Ω.
Dit levert duidelijk een serieschakeling, met vervangingsweerstand
$$R_{\text{schakeling}} = 30 + 14 = 44 \; \Omega.$$
Het is instructief om na te gaan hoe in een dergelijke schakelingen de spanningen en stroomsterktes berekend worden. Veronderstel dat zij wordt aangesloten op een spanningsbron van 15 volt.
De totale stroomsterkte door de schakeling is dan
$$I_{\text{schakeling}} = \frac{15 \; \text{V}}{44 \; \Omega} = 0{,}34 \; \text{A}.$$
Al deze stroom vloeit door de weerstand van 30 Ω (I1 = 0,34 A) en ook door de parallel combinatie (I23 = 0,34 A). Hieruit berekent men de spanningen:
$$U_1 = 0{,}34 \; \text{A} \cdot 30 \; \Omega = 10{,}2 \; \text{V}; \; \; U_2=0{,}34 \; \text{A} \cdot 14 \; \Omega = 4{,}8 \; \text{V}.$$
De spanning van 4,8 V staat over elk van de parallel geschakelde weerstanden, maar de stroom vertakt zich:
$$I_2 = \frac{4{,}8 \; \text{V}}{20 \; \Omega} = 0{,}24 \; \text{A}; \; \; \; I_3 = \frac{4{,}8 \; \text{V}}{50 \; \Omega} = 0{,}01 \; \text{A}.$$
Voorbeeld 2
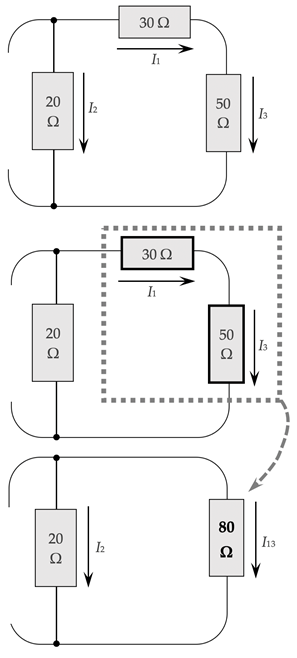
Hoewel de hier getekende schakeling lijkt op het voorgaande voorbeeld, is ze toch heel anders. Ditmaal vertakt de stroom zich onmiddellijk aan het begin, en komen de takken pas aan het einde samen.
De weerstanden van 30 Ω en 50 Ω bevinden zich in dezelfde tak; zij vormen een serieschakeling, met vervangingsweerstand
$$R_{13} = 30 + 50 = 80 \; \Omega.$$
Wij teken de schakeling opnieuw, maar vervangen de in serie geschakelde weerstanden door een enkele weerstand van 80 Ω. Het resultaat is een parallelschakeling, met vervangingsweerstand
$$\frac{1}{R_{\text{schakeling}}} = \frac{1}{20} + \frac{1}{80},$$
zodat Rschakeling = 16 Ω.
Opnieuw gaan we na wat er gebeurt als deze schakeling wordt aangesloten op een spanningsbron, van bijvoorbeeld 8,0 V. De stroomsterkte door de schakeling wordt
$$I_{\text{schakeling}} = \frac{8{,}0\; \text{V}}{16 \; \Omega} = 0{,}05 \; \text{A}.$$
De weerstand van 20 Ω heeft 8,0 V spanning en krijgt 0,40 A aan stroom. De overige 0,10 A stroomt door de rechtertak van de schakeling. Het is eenvoudig na te gaan dat de weerstand van 30 Ω een spanning heeft van 3,0 V en die van 50 Ω een spanning van 5,0 V.
