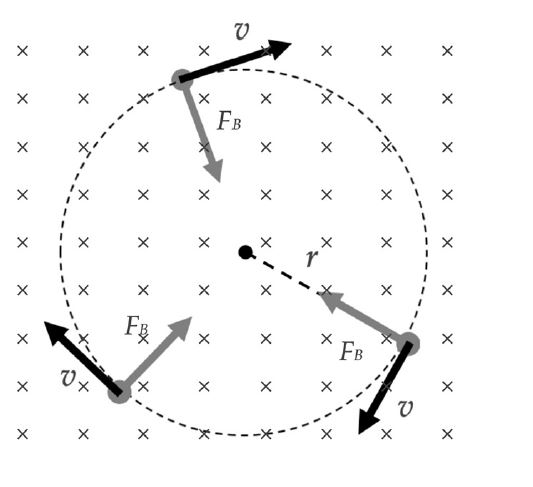
Als een geladen deeltje zich loodrecht beweegt op magnetische veldlijnen, zal het zich in een cirkelbaan bewegen. Dit is het gevolg van de Lorentzkracht, die steeds loodrechts op de beweging staat. Deze kracht functioneert hier als de centripetaalkracht (zie paragraaf 21.4).
De afbeelding illustreert dit. De kruisjes x geven aan dat het magnetische veld B van ons vandaan wijst, de pagina in. In dit veld beweegt zich een elektron, met de klok mee. Door de derde rechterhandregel te gebruiken zien wij, dat de Lorentzkracht FB steeds naar het midden van de cirkel wijst.
Stelt men de vergelijkingen voor de Lorentzkracht en de centripetaalkracht gelijk, dan kan men een formule afleiden voor de straal van de cirkelbaan (de cyclotronvergelijking):
$$q \; v \; B = \frac{v^2}{r} \Rightarrow r = \frac{ m\; v}{q \; B}.$$
Voorbeeld: Een zilverion ($q = +e = +1,6 \cdot 10^{-19} \; \text{C}; m = 1,8 \cdot 10^{-25} \; \text{kg}$) beweegt zich met een snelheid van 5000 m/s loodrecht op een de veldlijnen van een magneetveld B = 2,00 T. Bepaal de straal van de cirkelbaan.
$$r = \frac{m \; v}{q \; B} = \frac{1,8 \cdot 10^-25 \cdot 5000}{1,6 \cdot 10^{-19} \cdot 2,00} = 0,0028 \; \text{m} = 2,8 \; \text{mm}.$$
