In de beschrijving van elektromagnetische inductie wordt het begrip magnetische flux gebruikt. Deze grootheid is verwant, maar niet gelijk aan de magnetische veldsterkte B.
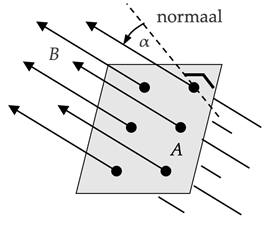
Conceptueel mag men magnetische flux beschouwen als een maat voor het aantal magnetische veldlijnen dat door een oppervlakte loopt. Nauwkeuriger wordt magnetische flux (Φ) gedefinieerd door de vergelijking
$$\Phi = B_\perp \cdot A.$$
Hierin is
- B⊥ de magnetische veldsterkte loodrecht op het oppervlak;
- A de grootte van het oppervlak waarvoor de flux bepaald moet worden;
- Φ de magnetische flux door het oppervlak.
(Men kan ook schrijven: $\Phi = B\cdot A\cdot \cos \alpha$, waarbij $\alpha$ de hoek is tussen het magnetische veld en de normaal van het oppervlak.)
Elektromagnetische inductie vindt plaats in het geval van verandering van flux in de spoel. Uit de definitie van flux is duidelijk dat dit gebeurt
- als de magnetische veldsterkte door een spoel verandert, bijvoorbeeld doordat de afstand tussen magneet en spoel verandert;
- als de richting van het magnetische veld ten opzichte van een spoel verandert, doordat een magneet of de spoel zelf gedraaid wordt;
- als de oppervlakte van een spoel verandert, doordat de spoel vervormd wordt.
Wanneer een magnetisch veld door een spoel gaat, draagt iedere winding bij aan de magnetische flux. Om de totale flux door de spoel te vinden, moet men dus de flux van een enkele winding vermenigvuldigen met het aantal windingen, N. Voor de totale flux door een spoel geldt: $$\Phi = N \cdot B_\perp \cdot A$$
Voorbeeld: Een spoel met een ronde doorsnede met een diameter van 6,0 cm en 500 windingen wordt geplaatst in een magnetisch veld van 30 mT. Hoe groot is de flux door de spoel als zijn as evenwijdig is aan het magnetische veld?
$$A = \pi \; r^2 = \pi \cdot (0,030 \; \text{m})^2 = 2,8 \cdot 10^{-3} \; \text{m}^2;$$
$$\Phi = N \; B \; A = 500 \cdot 0,030 \; \text{T} \cdot 2,8 \cdot 10^{-3} \; \text{m}^2 = 0,042 \; \text{Wb}.$$
