Een functie is een voorschrift dat aan elk getal een specifiek ander getal toekent.
$$x \overset{functie}{\rightarrow} y.$$
- x is de onafhankelijke variabele, de invoer, of het origineel.
- y is de afhankelijke variabele, de uitvoer, of het beeld.
Een functievoorschrift is een formule die vertelt hoe de uitvoer berekend wordt. Deze wordt geschreven als
$$y = …. \;\;\; of \;\;\; f(x) = …. \;\;\; of \;\;\; f: x \mapsto … \;\;\; of \;\;\; f: x \mapsto y(x) = …$$
Aan de hand van het functievoorschrift kan men van alles doen.
- Evalueer een functie: bereken de uitvoer y die bij een gegeven invoer x
- Oplossen van de functie: bereken de invoer x die een gegeven uitvoer y
- Maak een tabel, waarin voor een aantal invoerwaarden de bijbehorende uitvoer staat.
- Teken of schets de grafiek, die bestaat uit punten (x, y) van invoer en uitvoer die bij elkaar horen.
Gegeven is de functie:
$$f(x) = \frac{3x}{x^2 + 1}.$$
- Evalueer: f(–2). Vul x = –2 in het functievoorschrift in.
$$f(-2) = \frac{3 \cdot (-2)}{(-2)^2 + 1} = -1,2$$
- Maak een tabel van f. Hiervoor evalueren we voor een aantal x-waarden.

- Teken de grafiek van f. De tabel geeft zeven punten die de vorm goed weergeven.
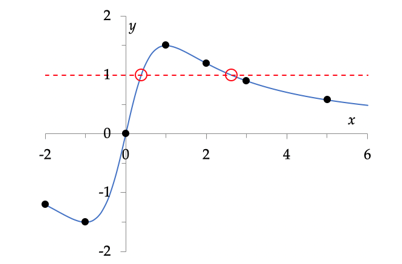
- Los op: f(x) = 1.
- De grafische oplossing is hierboven getoond: de lijn y = 1 is getekend als een stippellijn. Haar snijpunten met de grafiek geven aan dat er twee oplossingen zijn. Aflezen van de coördinaten laat zien x ≈ 0,4 of 2,6.
- De algebraïsche oplossing wordt gevonden door een vergelijking op te lossen:
$$1 = \frac{3x}{x^2+1} \Rightarrow x^2 – 3x + 1 = 0 \Rightarrow x = \frac{3 \pm \sqrt{5}}{2}$$
