Stel dat een vloeistof in evenwicht is. Nu brengen wij een verandering aan, bijvoorbeeld door ergens meer kracht op de vloeistof uit te oefenen. Hierdoor zal de druk in de vloeistof veranderen, niet alleen op de plaats waar de verandering plaatsvindt, maar overal. Er ontstaat een nieuw evenwicht.
Het beginsel van Pascal zegt nu, dat de druktoename of -afname is gelijk voor alle delen van de vloeistof.
Als bijvoorbeeld de druk in één punt toeneemt met 20 pascal, zal de druk overal toenemen met 20 pascal. (Merk op dat het beginsel niet zegt dat de druk overal gelijk is: zoals hierboven besproken, is er meer druk op grotere diepte.)
Een belangrijke toepassing van het beginsel van Pascal is de hydraulische lift. Men neemt twee verbonden vaten, één smal en één breed, en vult die met vloeistof. Bovenop de vloeistof plaats met zuigers die vrij op een neer kunnen bewegen. Op de brede zuiger wordt nu een last geplaatst, bijvoorbeeld een auto. Om deze last te kunnen dragen, moet de vloeistof in het brede vat nu meer druk uitoefenen op de zuiger. Volgens het beginsel van Pascal is hiervoor dezelfde drukverhoging nodig in het smalle vat. Vanwege de kleinere oppervlakte is hier echter minder kracht voor nodig.
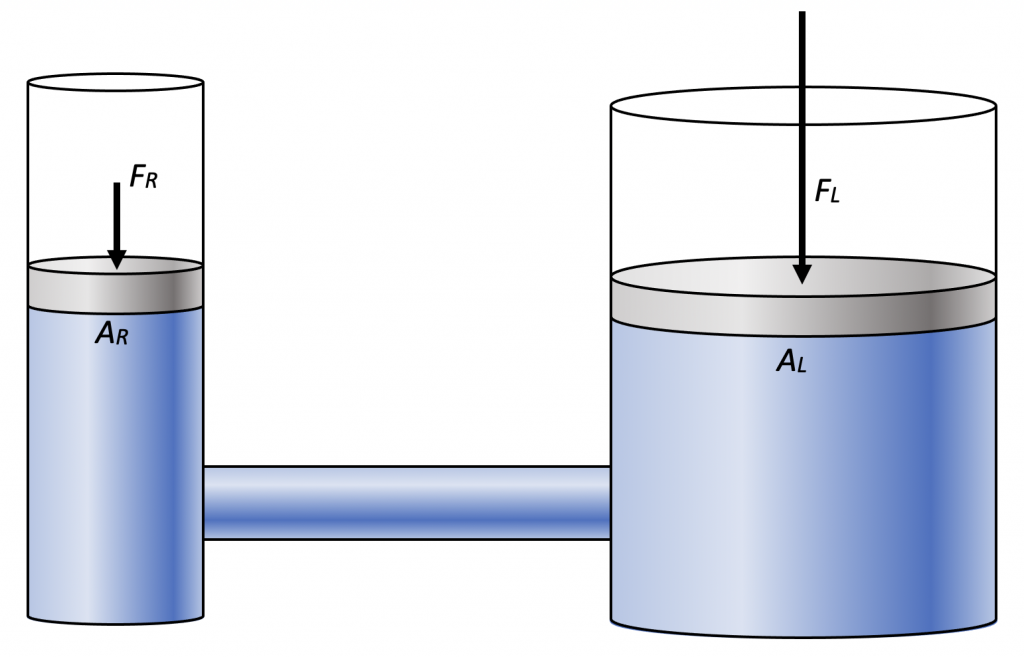
Stel dat AL en AR de oppervlakten van de zuigers zijn, en FL en FR zijn de neerwaartse krachten die op de zuigers werken. Dan geldt
$$\Delta p_L = \Delta p_R\ \ \ \ \text{(beginsel van Pascal)};$$
$$\frac{F_L}{A_L} = \frac{F_R}{A_R};$$
$$F_L=F_R \cdot \frac{A_L}{A_R}.$$
Als bijvoorbeeld het oppervlak van de brede zuiger 20 maal zo groot is als dat van de smalle zuiger (AL/AR = 1/20), dan is FL maar 1/20ste van FR.
