40.1.4 Stijgen en dalen

Als men de grafiek van een functie van links naar rechts doorloopt, ziet men de grafiek omhoog en omlaag gaan (stijgen en dalen). Dit komt overeen met toename en afname van de uitvoer voor toenemende invoer.

Meer precies kijkt men naar de raaklijn aan de grafiek. Op overgangspunten van stijgen naar dalen (en omgekeerd) loopt de raaklijn horizontaal.
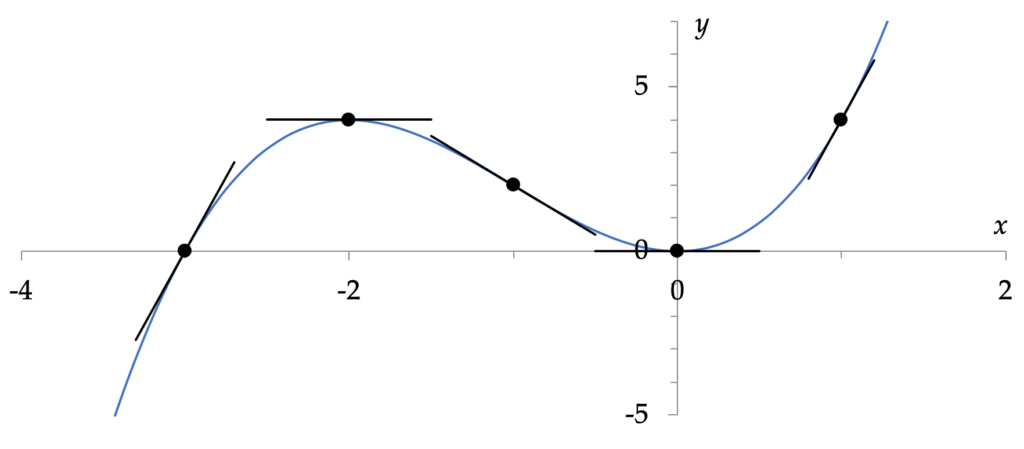
Voorbeeld: Getekend is de functie f(x) = x3 + 3×2.

Van links naar rechts ziet men deze functie stijgen, tot x = –2, waar de grafiek een horizontale raaklijn heeft. Daarna daalt de grafiek, tot x = 0. Na x = 0 stijgt de grafiek weer.
Men kan het stijgen en dalen bestuderen aan de hand van het tekenverloop van de afgeleide functie.

• f'(x) > 0                 functie stijgt
• f'(x) < 0                 functie daalt
• f(x) = 0                 raaklijn is horizontaal  

Een maximum treedt op waar de uitvoer groter is dan voor andere invoerwaarden. In een relatief maximum is de uitvoer groter dan voor naburige invoerwaarden. Op dezelfde manier definieert men een (relatief) minimum.

Deze extrema treden meestal op

• in randpunt van het domein;
• in punten waar een functie discontinu is;
• als f'(x) = 0
  • Als de functie van stijgen naar dalen overgaat, is er een relatief maximum.
  • Als de functie van dalen naar stijgen overgaat, is er een relatief minimum.
  • Anders is er sprake van een horizontaal buigpunt.

Voorbeelden:

• Bestudeer het stijg- en daalgedrag van f(x) = x³ + 3x².
  • De afgeleide is f'(x) = 3x² + 6x
  • Bijvoorbeeld: als x = –1 dan is f'(-1) = -3
    Dus als x = –1 heeft de raaklijn hellinggetal –3, dus vrij steil omlaag.
  • Het tekenverloop van de afgeleide functie is
• 
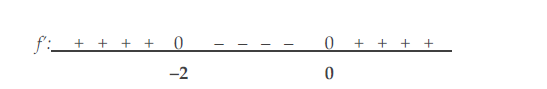
  • Hieruit volt onmiddellijk het stijg- en daalgedrag van de functie f:
    
• Bestudeer het stijg- en daalgedrag van $f(x) = x^4 – 3x^2 -1$.
  • De afgeleide is $f'(x) = 4x^3 – 6x$.
  • De nulpunten van de afgeleiden: $$4x^3 – 6x =0 $$ $$(4x^2 – 6) \cdot x = 0$$ $$4x^2 = 6 \; \text {of} \; x = 0$$ $$x = \pm \frac{1}{2} \sqrt{3} \; \text{of} \; x = 0.$$

• In deze drie punten heeft de functie dus waarschijnlijk extrema. Door bijvoorbeeld x = –2, –1, +1, +2 in te vullen vinden wij het tekenverloop van de eerste afgeleide:
  
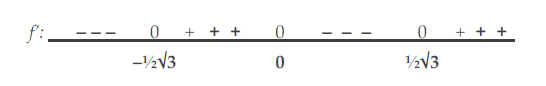
  Het stijg- en daalgedrag van de functie f zelf is derhalve: