Wanneer een projectiel opwaarts geworpen wordt, zal het eerst een tijdje omhoog bewegen. Op het hoogste punt van de baan keert het om en valt het naar beneden.
In dit geval is het gebruikelijk de positieve y-richting omhoog te kiezen, zodat de beginsnelheid v0 positief is, maar de versnelling negatief: ac = –g. De vergelijkingen voor EVRB worden nu:
$$v = v_0 – \; g \; t$$
$$y = v_0 \; t -\; \frac{1}{2}g \; t^2$$
(eventueel $+ y_0$ als de beginhoogte niet nul is.)
De volgende vragen zijn vaak belang in deze situatie:
Wanneer wordt het hoogste punt bereikt?
Op het hoogste punt van de beweging is v = 0, aangezien het teken bezig is op te keren van + naar –. Men gebruikt dit feit in de eerste vergelijking en lost op voor t:
$0 = v_0 \; – g \; t \Rightarrow t = …$ (op het hoogste punt)
Hoe hoog is dat hoogste punt?
Als eenmaal bekend is wanneer dit punt bereikt wordt, kan men de gevonden waarde voor t in de vergelijking voor y invullen.
Hoe lang duurt het voor het voorwerp terugkeert tot zijn oorspronkelijke hoogte?
Het terugvallen naar de oorspronkelijke hoogte duurt even langs als de opwaartse beweging. Als het hoogste punt bereikt wordt op tijdstip t, wordt de oorspronkelijke hoogte dus weer aangedaan op 2t.
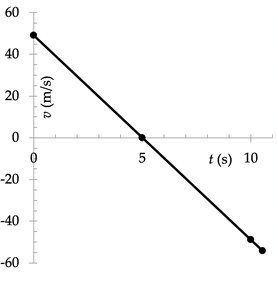
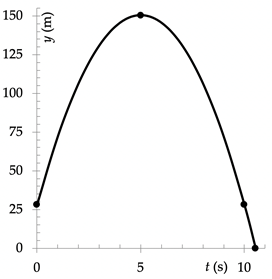
Voorbeeld: Een speelgoedraket wordt afgeschoten vanaf de rand het hoge dak van de school, 28,0 meter boven de grond. De raket wordt vrijwel recht omhoog gelanceerd, met een beginsnelheid van 49 m/s. Neem aan (niet al te realistisch) dat luchtweerstand geen rol speelt. Beschrijf de belangrijkste aspecten van de beweging van de raket, tot aan het moment dat deze op de grond terecht komt.
De vergelijkingen voor de raket zijn
$$v = 49 \; – 9,8 \cdot t;$$
$$y = 28,0 + 49 \cdot t \; – 4,9 \cdot t^2.$$
Het hoogste punt wordt bereikt wanneer v = 0:
$$0 = 49 \; – 9,8 \cdot t \Rightarrow t = 5,0 \; \text{s}.$$
Dus duurt het vijf seconden om het hoogste punt te bereiken. De hoogte op dit moment is
$$y = 28,0 + 49 \cdot 5,0 \; – 4,9 \cdot 5,0^2 = 151 \; \text{m}.$$
Dit is de grootste hoogte, gemeten vanaf de grond.
De raket valt langs de rand van het dak (de oorspronkelijke hoogte) na nogmaals vijf seconden. Op t = 10,0 s hebben wij dus y = 28,0 m. Het is eenvoudig na te gaan dat de raket nu weer een snelheid heeft van 49 m/s, maar dan in neerwaartse richting.
Tenslotte, om te bepalen wanneer de raket op de grond landt, stellen we y = 0 en lossen op voor t. Dit is een kwadratische vergelijking:
$0 = 28,0 + 49 \cdot t \; – 4,9 \cdot t^2$.
De oplossingen hiervan blijken te zijn t = –0,54 s en t = +10,54 s. Het is duidelijk dat wij de positieve oplossing moeten hebben: 10,54 seconden na de lancering valt de raket op de grond. Invullen in de vergelijking voor v laat zien, dat de raket de grond raakt met een neerwaartse snelheid van –54 m/s.