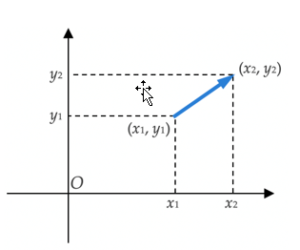
Stel dat twee punten gegeven zijn, met coördinaten (x1, y1) en (x2, y2). De relatieve ligging van deze punten kan worden beschreven middels hun afstand en hun richting. In de tekening hieronder is deze relatieve ligging aangegeven door een pijl. Deze pijl heet ook wel de vector van het ene naar het andere punt.
Het is nuttig om eerst de “delta’s” te definiëren
∆x = x2 – x1; ∆y = y2 – y1.
De afstand tussen de punten volgt m.b.v. de stelling van Pythagoras:
$\text{afstand} = \sqrt{(\Delta x)^2 + (\Delta y)^2}= \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}.$
De relatieve richting tussen de punten wordt meestal uitgedrukt met behulp van het hellinggetal of richtingscoëfficiënt (ri.co.). Deze beschrijft de “steilheid” van de vector.
$\text{ri.co} = \frac{\Delta y}{\Delta x} = \frac{y_2 – y_1}{x_2 – x_1}.$
Voorbeeld: Bepaal de afstand en het hellinggetal voor de punten (–2, 3) en (10, –4).
$\Delta x = 10 – (-2) = +12.$<.=/p>
$\Delta y = (-4)-3 = -7;$
$\text{afstand} = \sqrt{(+12)^2 + (-7)^2} = \sqrt{144 + 49} = 17;$
$\text{ri.co} = \frac{-7}{12}\approx =0{,}583.$
