Stel dat de coördinaten van twee punten gegeven zijn, als (x1, y1) en (x2, y2). Gevraagd wordt een vergelijking te bepalen voor de lijn die door deze punten loopt. Om dit probleem op te lossen moeten de parameters bepaald worden in de vergelijking y = Ax + B.
Het hellinggetal is
$A = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2 – x_1}.$
Als dit eenmaal bepaald is, kan de waarde van B gevonden worden door de coördinaten van één van de punten in de vergelijking in te vullen, en die op te lossen voor B.
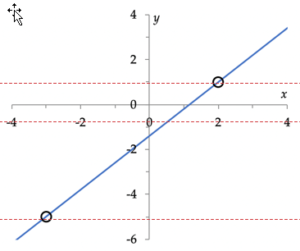
Voorbeeld: Bepaal de vergelijking voor de hier getekende lijn, die gaat door (–3, –5) en (2, 1).
$A= \frac{y_2-y_1}{x_2 – x_1}= \frac{1-(-5)}{2-(-3)} = \frac{6}{5}.$
We berekenen B door het punt (–3, –5) in de vergelijking in te vullen:
$y = \frac{6}{5}x + B$
$-5 = \frac{6}{5} \cdot (-3) + B$
$-5 = \frac{-18}{5} + B$
$B= -5 – \frac{-18}{5} = -\frac{7}{5}$
Dus heeft de lijn de vergelijking
$y=\frac{6}{5}x – \frac{7}{5}$
