Twee lijnen die niet evenwijdig lopen snijden elkaar in één punt. Een belangrijk probleem in de analytische meetkunde is het bepalen van de coördinaten van dat snijpunt als vergelijkingen voor de lijnen gegeven zijn.
Het snijpunt (x, y) ligt op beide lijnen, en voldoet daarom aan beide vergelijkingen. Derhalve komt het vinden van het snijpunt neer op het oplossen van een stelsel van twee vergelijkingen.
Als standaardvergelijkingen van de lijnen zijn gegeven, kan men die eenvoudigweg gelijkstellen. Dit levert een lineaire vergelijking in x.
Voorbeeld: Bepaal het snijpunt van
lijn 1: y = –4x + 2;
lijn 2: y = 2x – 3.
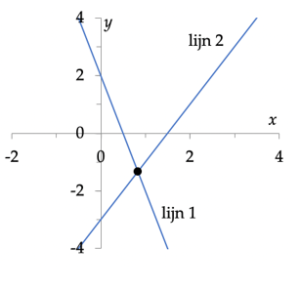
Als de uitdrukkingen aan de rechterkant gelijk zijn aan dezelfde y-waarde, moeten ze gelijk zijn aan elkaar. We kunnen daarom schrijven
$-4x + 2 = 2x – 3;$
de oplossing is eenvoudig te vinden:
$-6xx = -5, \;\;\; x = \frac{5}{5}$
De y-waarde kan worden gevonden uit elk van de gegeven vergelijkingen:
$y = -4 \cdot \frac{5}{6} + 2 = -3\frac{1}{3} + 2 = -1\frac{1}{3}$
$y = 2 \cdot \frac{5}{6} -3 = 1\frac{2}{3} – 3 = -1 \frac{1}{3}$ (ter controle!)
Zodoende is het snijpunt van deze lijnen het punt $(\frac{5}{6}, -1\frac{1}{3}$
