Door een kwadraat af te splitsen kan de vergelijking voor de parabool ook geschreven worden in de vorm
$y = A(x-u)^2 + v$
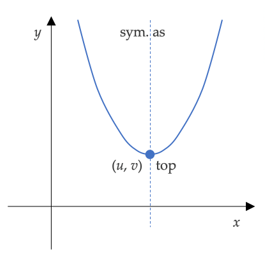
De getallen (u, v) zijn de coördinaten van de top.
Voorbeeld: Bepaal de top van de parabool met vergelijking $y = -2x^2 + 12x – 10$.
$y = -2 \cdot (x – …)^2 – …$ gewenste vorm
$y = -2 \cdot (x-3)^2 – …$ dit is gelijk aan –2x2 + 12x – 18
$y = -2 \cdot (x-3)^2 + 8$ want –18 + 8 = –10.
Lees de coördinaten van de top nu af: (u, v) = (3, 8). De negatieve waarde A = –2 laat zien dat de parabool naar onder toe open is.
