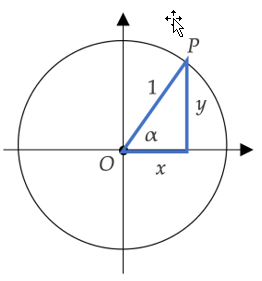
Door in de eenheidscirkel een handige driehoek te tekenen, kan men zien dat de coördinaten van een punt P op de eenheidscirkel verband houden met de trigonometrische verhoudingen: $$x = \sin{\alpha}$$ $$y = \sin{\alpha}$$ $$\mathrm{ri. \; co. \; van} \; OP = \frac{y}{x} = \tan{\alpha}$$
Deze drie vergelijkingen kunnen beschouwd worden als alternatieve definities van de goniometrische verhoudingen sin, cos, en tan. Het is nu ook duidelijk hoe deze verhoudingen kunnen worden gedefinieerd voor hoeken kleiner dan 0˚ of groter dan 90˚, d.i. in andere kwadranten. Om de sinus, cosinus en tangens van zulke hoeken te berekenen, voert men spiegelingen uit in de eenheidscirkel zodat men in het eerste kwadrant terecht komt:
- spiegeling in de x-as: $\alpha \rightarrow – \alpha \mathrm{\; of \;} 360^\circ – \alpha\;\;\; [2\pi – \alpha]$
- spiegeling in de y-as: $\alpha \rightarrow 180^\circ – \alpha\;\;\; [\pi – \alpha]$
- puntspiegeling in de oorsprong: $\alpha \rightarrow \alpha \pm 180^\circ \;\;\; [\alpha \pm \pi]$
Bereken sin 150˚.
- Deze hoek ligt in kwadrant II, dus de sinus (y-coördinaat) is positief.
- Spiegelen om de y-as brengt ons naar 180˚ – 150˚ = 30˚.
- Omdat sin 30˚ = ½, is sin 150˚ = ½.
Bereken cos 1¼π.
- Deze hoek ligt in kwadrant III, dus de cosinus (x-coördinaat) is negatief.
- Puntspiegeling brengt ons naar 1¼π – π = ¼π (45˚).
- Omdat cos ¼π = ½√2, is cos 1¼π = –½√2.
Bereken tan (–60˚).
- Deze hoek ligt in kwadrant IV, dus de tangens (ri.co.) is negatief.
- Spiegeling om de x-as brengt ons naar –(–60˚) = 60˚.
- Omdat tan 60˚ = √3, is tan 60˚ = –√3.
