Als f gelijk is aan de afgeleide van F, dan is F een primitieve (functie) ofwel een oneigenlijke integraal van f. Dit wordt genoteerd als $\int f(x)dx$. Derhalve, $$F(x) = \int f(x)dx \Leftrightarrow f(x) = F'(x).$$
Om te controleren of F een primitieve is van f, behoeft men slechts F te differentiëren.
Als $\int (6x^4 + e^{3x} = Ax^5 +Be^{3x}$, hoe groot zijn de getallen A en B?
We bepalen de afgeleide van de gegeven primitieve:
$$F(x) = Ax^5 + Be^{3x} \Leftrightarrow F'(x) = 5Ax^4 + 3Be^{3x}$$
Om dit gelijk te maken aan $f(x) = 6x^4 + e^{3x}$, moeten we dus kiezen A = $\frac{6}{5}$ en B = \frac{1}{3}$.
De primitieve van een functie f is niet uniek. Men kan immers een constante bij een functie optellen zonder dat de afgeleide verandert; daarom is een primitieve functie slechts bepaald op een integratieconstante na. Deze constante kan vrij gekozen worden; binnen een berekening van een integraal moet men echter wel consequent dezelfde constante gebruiken.
Voortbouwend op bovenstaand voorbeeld,
$\int (6x^4 + e^{3x})cs = \frac{6}{5} x^5 + \frac{1}{3}e^{3x} + C$
waarbij C de integratieconstante is.
Soms kan men de primitieve van een functie bepalen door de tabel van afgeleiden in paragraaf 39.3. in omgekeerde richting te gebruiken. In andere gevallen is het (veel) ingewikkelder. De volgende tabel geeft de primitieve van veel gebruikte standaardfuncties.
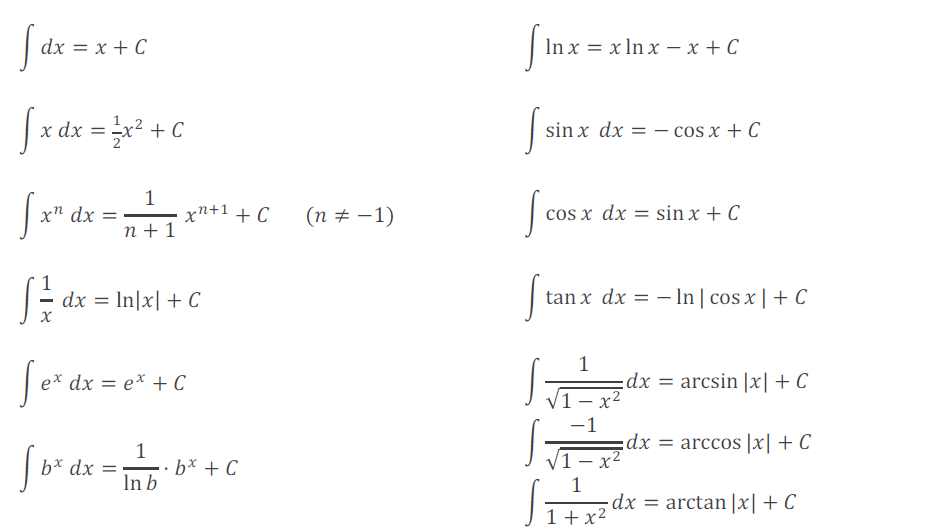
Helaas zijn de rekenregels voor integreren moeilijker dan voor differentiëren: er bestaan geen productregel, quotiëntregel of kettingregel die direct kan worden ingezet. Wel geldt:
- Optellen, aftrekken, en vermenigvuldiging met een constante vertalen direct door naar de integraal:
- $\int (f(x) \pm g(x)) dx = \int f(x) dx \pm \int g(x) dx$
- $\int A \cdot f(x)dx = A \cdot \int f(x) dx$
- Als het argument x van een functie is vermenigvuldigd met een constante B, dan moet de integraal gedeeld worden door B:
- $\int f(x) dx = F(x) \Rightarrow \int f(Bx) dx = \frac{1}{B}\cdot F(Bx)$
- Het optellen of aftrekken van een constante B bij het argument x kan gewoon worden “doorvertaald”:
- $\int f(x) dx = F(x) \Rightarrow \int f(x+B)dx = F(x+B).$
(Er bestaan vele andere technieken en regels voor integreren, die hier niet worden behandeld. Over het algemeen is integreren veel lastiger dan differentiëren. Zo kan de primitieve van de belangrijke functie $f(x) = e^{\frac{-x^2}{2}$ niet eens worden geschreven als een formulefunctie!)
$ \int(8x^3 – \sin{5x} $
$= 8 \cdot (\frac{1}{4} \cdot x^4) – \frac{1}{5} \cdot (- \cos{5x}) $
$= 2x^4 + \frac{1}{5} \cos{5x} + C$
$\cos{(3x -2)} dx $
$ = \sin{(3x-2)} + C$
$\int e^{-\frac{x}{4}} dx $
$= -4e^{-\frac{x}{4}} + C$
En een aardig trucje voor rationele functies:
$\int \frac{dx}{x^2 – 5x + 4} $
$= \int \frac{dx}{(x-4)(x-1} $
$ = \int \frac{1}{3}(\frac{1}{x-4} – \frac{1}{x-1})dx$$
$= \frac{1}{3} (\ln |x – 4 | – \ln |x -1|) +C$
