Lineaire (eerstegraads-) functies werden al besproken in paragraaf 35.1. Hun grafiek is een rechte lijn.
Kwadratische (tweedegraads-) functies werden in feite behandeld in paragraaf 37.3. Hun grafiek is een orthogonale parabool. Er is altijd één maximum of minimum: de top. Voor het vinden van de nulpunten lost men een kwadratische vergelijking op: zie paragraaf 2.2.
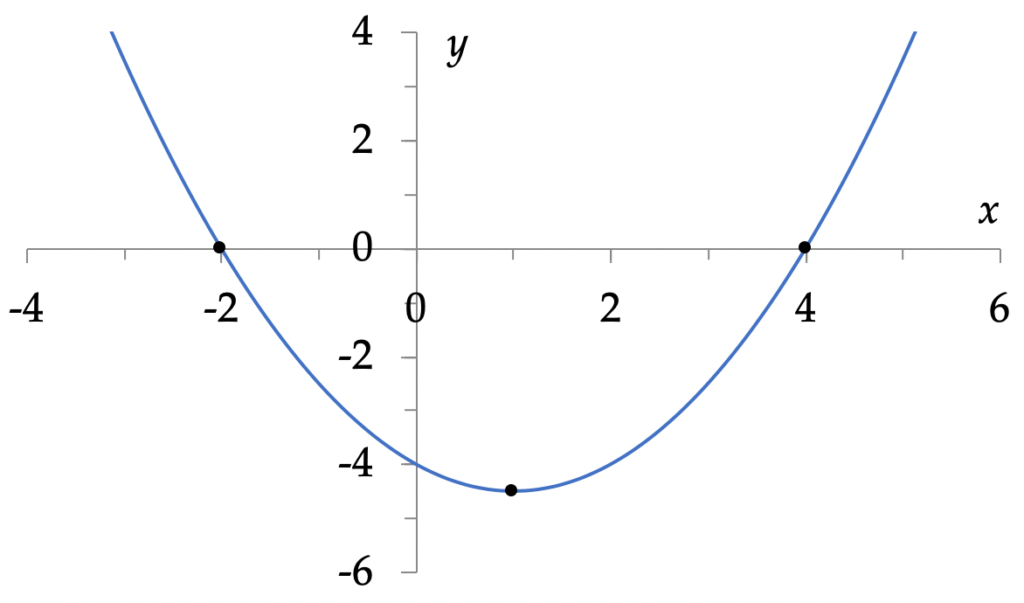
Onderzoek $f(x) = \frac{1}{2} x^2 – x – 4$
Domein: alle reële getallen.
De grafiek is een parabool. Omdat A = ½ positief is, is de parabool open naar boven toe. De grafiek is dus overal hol.
Nulpunten:
$\frac{1}{2} x^2 – x- – 4 = 0$
$x^2 – 2x – 8 = 0 \;\;\;\; \text{met 2 vermenigvuldigd}$
$(x-4)\cdot (x+2) = 0 \;\;\;\; \text{ontbonden in factoren}$
$x = -2 \text{of} x = 4$
Eerste afgeleide: $f'(x) = x-1$
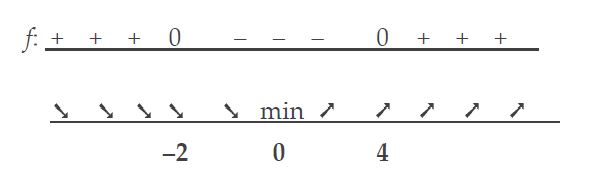
Nulpunt van de afgeleide: x = 1. De afgeleide veranderd hier van – naar +, dus is dit een minimum met waarde f(1) = –4½. De top ligt dus op (1, –4½).
Tekenverloop: