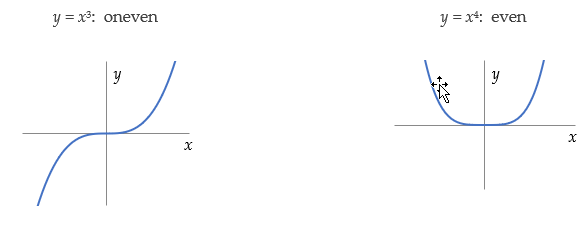Over veeltermfuncties van graad 3 en hoger wordt het al moeilijker algemene uitspraken te doen. De eenvoudigste gevallen zijn machtsfuncties, met alleen een term van graad n:
$$f(x) = A \cdot x^n \;\;\;(A>0, \; n \text{ een positief geheel getal)}$$
Deze functies hebben een bepaalde symmetrie:
- Als n oneven is, geldt $f(-x) = -x$. De grafiek is puntsymmetrisch in de oorsprong.
- Als n even is, geldt $f(-x) = x$. De grafiek is lijnsymmetrisch in de y-as.