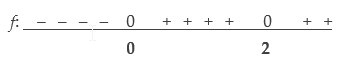Een nulpunt van een functie f is een invoerwaarde x waarbij de uitvoer nul is. Dit zijn de x-waarden waar de grafiek de horizontale as snijdt. Men vindt de nulpunten door f(x) = 0 op te lossen.
Het tekenverloop van een functie f beschrijft voor welke invoerwaarden x de functie positieve en negatieve uitvoerwaarden levert. De meeste functies zijn continu, zodat er geen “sprongen” in de uitvoer zitten. Het omslaan van een teken (– naar +, of + naar –) gebeurt dan alleen bij een nulpunt of bij een gat in het domein. Om het tekenverloop te bepalen gaat men dus als volgt te werk:
- teken een getallenlijn
- bepaal het domein; markeer alle waarden en intervallen die buiten het domein vallen
- bepaal de nulpunten; markeer deze op de getallenlijn
- kies voor elk stukje getallenlijn een waarde x en bereken of f(x) > 0 dan wel < 0.
Beschrijf het tekenverloop van f(x) = x3 – 4x2 + 4x.
- Het domein bestaat uit alle reële getallen.
- Om de nulpunten te vinden, lossen we op
x^3 – 4x^2 + 4x \Rightarrow x = 0 \; \text{of} x = 2
f: 0 0
0 2
- Bereken de uitvoer voor waarden in de drie stukjes van het domein:
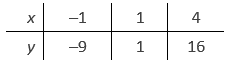
- Het tekenverloop van deze functie is dus als volgt: