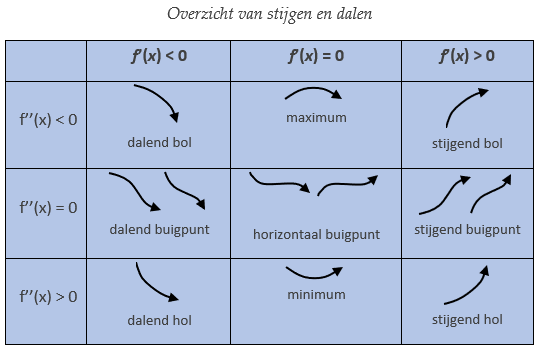
De grafiek van een functie is hol of concaaf als zij (gezien van links naar rechts) steeds sterker stijgt of steeds minder sterk daalt. De grafiek is bol of convex als zij steeds minder sterk stijgt of steeds sterker daalt.
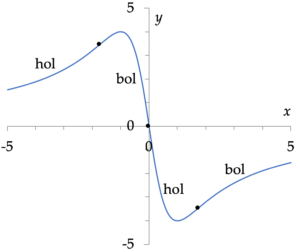
Voorbeeld: $$f(x) = \frac{-8x}{x^2+1}$$
Deze grafiek stijgt steeds sterker (is hol) tot ongeveer x ≈ –1,8. Daarna stijgt zij minder en begint te dalen: de grafiek is bol tot aan x = 0. Tussen x = 0 en x ≈ 1,8 wordt de daling minder en begint te stijgen: de grafiek is weer hol. Tenslotte neemt na x ≈ 1,8 de stijging af; daar is de grafiek weer bol.
Het hol- en bol-zijn van de grafiek wordt nauwkeurig beschreven door de tweede afgeleide van een functie (geschreven als f ’’).
- f ’’(x) > 0 de grafiek is hol
- f ’’(x) < 0 de grafiek is bol
- f ’’(x) = 0 buigpunt
De tweede afgeleide wordt berekend door de eerste afgeleide nogmaals te differentiëren.
Voorbeeld: Beschouw de functie f(x) = x2 – 1/x. De eerste en tweede afgeleide zijn $$f'(x) = 2x + \frac{1}{2x}$$ $$f”(x) = 2 – \frac{2}{x^3}$$
Het tekenverloop van de tweede afgeleide is als volgt:
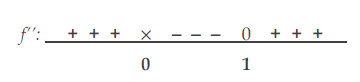 ( x is een gat in het domein )
( x is een gat in het domein )
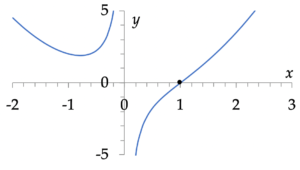
Dit betekent dat de grafiek van f
- hol is als x < 0
- bol is als 0 < x < 1
- een buigpunt heeft in x = 1
- weer hol is als x > 1.
Een buigpunt treedt op waar een grafiek van hol naar bol verandert, of omgekeerd. Een buigpunt is meestal een punt waar de grafiek haar grootste of kleinste mate van steilheid bereikt.