De antwoorden op deze opgaven zijn te vinden in het downloadbestand.
1 In bijgaande grafiek staat de trilling van een veer beschreven. 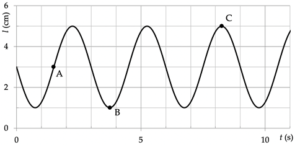
a. Wat is de amplitude?
b. Wat is de frequentie?
c. Wat is de fasehoek in punten A, B en C (tussen 0˚ en 360˚)?
d. Voorspel de lengte van de veer als t = 24,75 s.
2 Twee schommels bewegen heen en weer, volgens de vergelijkingen
schommel 1: $x = 2,0 \sin{(1,2t+1)}$
schommel 2: $x = 2,5 \sin{(0,8t – 1)} \;\;\;$(x in m, t in s).
3 Het eind van een strakgespannen touw wordt vijf keer per seconde omhoog en omlaag bewogen. Hierdoor ontstaat een golfpatroon, waarbij de toppen 48 cm uit elkaar liggen.
a. Wat is de periode van de golf?
b. Wat is de golfsnelheid in het touw?
c. Als het touw strakker gespannen wordt, verdubbelt de golfsnelheid. Wat gebeurt er met het golfpatroon?
4 Een kind van 60 kg hangt onderaan een gigantische springveer. De veer gaat elke 2,4 seconden een keer op en neer. Voorspel wat er gebeurt met deze periode als twee andere kinderen, elk 50 kg, er bij komen hangen.
5 Wanneer een gitarist een snaar bespeelt, ontstaat er een staande golf met één buik en twee knopen aan het eind. Houdt zij haar vinger echter licht op de snaar bij de 7e fret, dan ontstaat er een trillingspatroon met drie buiken en vier knopen. Als de oorspronkelijke trilling een frequentie had van 320 Hz, wat is de frequentie van de nieuwe trilling?
