Bij een roetsjbaan rijdt een voertuig op een spoor dat allerlei bochten heeft, zowel horizontaal als verticaal. Meestal wordt het voertuig eerst naar boven gebracht met behulp van een motor; daarna rijdt het naar beneden, slechts beïnvloed door twee krachten:
- de zwaartekracht door de aarde, in neerwaartse richting;
- de normaalkracht van het spoor, in een richting loodrecht op het spoor.
(Vooralsnog negeren wij wrijvings- en luchtweerstandskrachten.)
Deze situatie lijkt veel op die van het voorwerp op de helling (zie eerder in deze les); maar omdat er nu geen constante hellingshoek is, verandert de normaalkracht voortdurend en daarmee ook de versnelling van het voertuig. De theorie van eenparig versnelde beweging is niet meer van toepassing; bovendien zijn de precieze details over de vorm van het spoor vaak onbekend.
Toch kunnen wij één en ander zeggen over de beweging van het voertuig, door middel van een energie-analyse.
- Zolang het voertuig het spoor volgt, staat de normaalkracht altijd loodrecht op de bewegingsrichting. Dus verricht zij geen arbeid.
- De enige kracht die arbeid verricht op het voertuig is de zwaartekracht. Omdat deze kracht conservatief is, mogen wij de wet van behoud van mechanische energie toepassen.
$$K_{na} + U_{z,na} = K_{voor} + U_{z,voor}$$
$$\frac{1}{2}mv^2_{na} + mgy_{na} = \frac{1}{2}mv^2_{voor} + mgy_{voor}.$$
Men kan ook een tabel maken voor “energieboekhouding”; de totalen moeten gelijk zijn:
| voor | na | |
|---|---|---|
| kinetische energie $K = \frac 12 m v^2$ | … J | … J |
| potentiële energie $U = m g h$ | … J | … J |
| totale energie | … J | … J |
De massa m kan eventueel worden uitgedeeld uit bovenstaande vergelijking. Dit laat zien dat de beweging van het voertuig niet afhangt van zijn massa. (Dit verandert als luchtweerstand een grote rol gaat spelen.)
Voor de situaties “voor” en “na” kan men in principe elk willekeurig moment kiezen in de beweging van het voertuig. De totale mechanische energie is namelijk constant gedurende de hele rit.
Hieronder is dit alles toegepast voor een concreet geval. Het voertuig heeft een massa van 400 kg, en begint links op een hoogte van 30 m met een snelheid van 0 m/s.
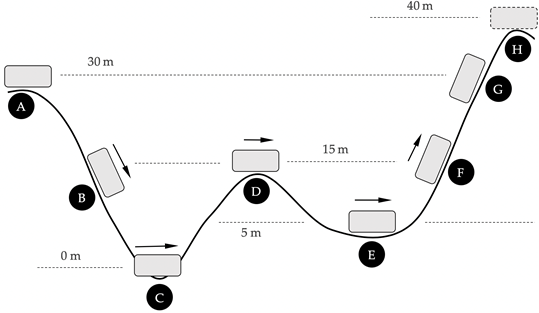
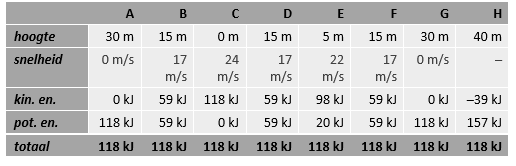
Merk op:
- Als het voertuig terugkomt naar dezelfde hoogte, zal het ook weer dezelfde snelheid hebben.
- Het voertuig kan nooit punt H bereiken. Dan zou de kinetische energie namelijk negatief moeten zijn, en dat is onmogelijk. Het voertuig zal omhoog gaan tot punt G, waar het tot rust komt, omkeert, en weer naar beneden rolt.
- Als er wrijving bestaat tussen het voertuig en het spoor, leidt dit tot niet-conservatieve negatieve. Hierdoor neemt de totale mechanische energie langzaam maar zeker af; het voertuig zal niet meer in staat zijn zijn oorspronkelijke hoogte te bereiken.
Voorbeeld: Stel dat op het boven beschreven voertuig wrijvingskrachten werken, die –38 kilojoule aan arbeid verrichten. Welke hoogte kan het voertuig nu maximaal bereiken?
De vergelijking voor energiebehoud wordt nu
$$\frac{1}{2}mv^2_{na} + mgy_{na} = \frac{1}{2}mv^2_{voor} + mgy_{voor} + W_{nc}.$$
Het voertuig was oorspronkelijk in rust, en wij moeten bepalen op welke hoogte het weer tot rust zou komen; dus is vna = vvoor = 0. Wat overblijft is:
$$m \; g \; y_{na} = m \; g \; y_{voor} + W_{nc};$$
$$y_{na} = y_{voor} + \frac{W_{nc}}{m \; g} = 30 + \frac{-38 \cdot 10^3}{400 \cdot 9,8} = 20,3 \; \text{m}.$$
