De stelling van Pythagoras: In een rechthoekige driehoek geldt
(schuine zijde)2 = (rechthoekzijde 1)2 + (rechthoekzijde 2)2.
Voorbeeld: In een rechthoekige driehoek is de kortste zijde 16 cm en de langste zijde 34 cm. Bepaal de ontbrekende zijde.
- De langste zijde moet de schuine zijde zijn. Dus:
(34 cm)2 = (16 cm)2 + x2; stelling van Pythagoras
x2 = 342 – 162; oplossen voor x2
$x = \sqrt{1156 – 256} = 30$ (positieve) vierkantswortel
Oppervlakte van een driehoek:
- Een rechthoekige driehoek (met rechthoekszijden a en b) kan
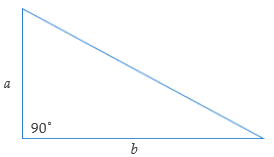worden beschouwd als de helft van een rechthoek met zijden van die lengte. Dus is de oppervlakte van de driehoek de helft van die van de rechthoek:
$$\text{opp} \; = \frac{1}{2} \cdot a \cdot b$$
- De oppervlakte van een willekeurige driehoek wordt meestal uitgedrukt als
$$\text{opp} \; = \frac{1}{2} \cdot \; \text{basis} \cdot \; \text{hoogte}$$
waarbij “basis” de lengte is van een zijde, en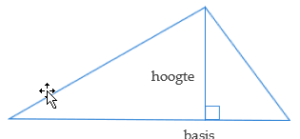
“hoogte” de lengte van de hoogtelijn die loodrecht is neergelaten op die zijde vanuit het tegenoverliggende hoekpunt.
- De formule van Heron: Als a, b, c de zijden van een driehoek zijn, berekent men eerst de halve omtrek, s:
$$s = \frac{1}{2} (a + b + c)$$ $$\text{opp} \; = \sqrt{s \cdot (s-a) \cdot (s-b) \cdot (s-c)}. $$
Voorbeeld: Wat is de oppervlakte van deze driehoek?
- Het lijnstuk van lengte 4 staat loodrecht op de zijde van
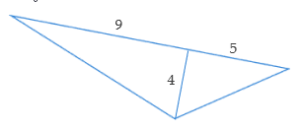lengte 9 + 5 = 14, en is dus een hoogtelijn.
$$\text{opp} = \frac{1}{2} \cdot \; \text{basis} \cdot \; \text{hoogte} = \frac{1}{2} \cdot 14 \cdot 4 = 28$$
