Wanneer een parabool wordt gesneden door een lijn, of door een andere parabool, dan zijn er nul, één, of twee snijpunten.
Wanneer expliciete vergelijkingen (in de vorm y = …) gegeven zijn, kan men deze snijpunten vinden door de vergelijkingen gelijk te stellen. Er ontstaat een kwadratische vergelijking, die kan worden opgelost.
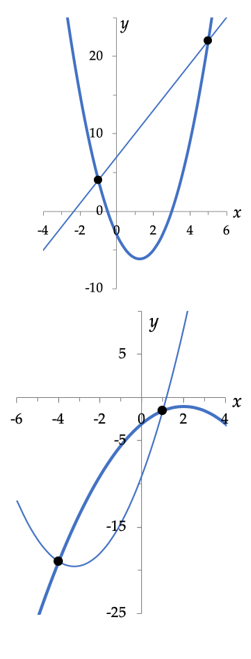
Voorbeeld: Bepaal het snijpunt van de lijn y = 3x + 7 met de parabool y = 2x2 – 5x – 3.
Gelijkstellen:
$3x + 7 = 2x^2 – 5x – 3$
$0 = 2x^2 – 8x -10$
$0 = x^2 – 4x – 5 = (x-5)(x+1)$
$x = -1 \; \text{of} \; 5$
$(x,y) = (-1,4) \; \text{of} \; (5,22)$
Voorbeeld: Bepaal het snijpunt van de parabolen y = –½x2 + 2x – 3 en y = x2 + 6½x – 9:
$-\frac{1}{2}x^2 + 2x – 3 = x^2 + 6\frac{1}{2}x – 9$
$0 = 1 \frac{1}{2}x^2 + 4 \frac{1}{2}x – 6$
$0 = x^2 + 3x – 4 = (x+4)(x-1)$
$x = -4 \;\text{of} \; 1$
$(x,y) = (-4, -19) \; \text{of} \; (1, -1\frac{1}{2})$
