Stel, men evalueert een functie f voor een rij invoerwaarden die een bepaald getal a steeds meer benaderen. Vaak zullen de bijbehorende uitvoerwaarden ook steeds dichter bij een bepaalde waarde komen te liggen. Deze heet de limiet van de functie voor a; we schrijven $\underset{x \rightarrow a}{lim} f (x)$.
Gegeven is de functie $$f(x) = \frac{2x}{x – x^2}$$
Evalueren in x = 0 mag niet, omdat er dan door nul gedeeld zou worden. Nu nemen wij echter een rij waarden die naar nul nadert:
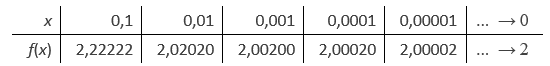
De uitvoerwaarden komen steeds dichter te liggen bij de waarde 2. Dus: $\underset{x \rightarrow 0}{\lim} f(x)$.
In de meeste punten zijn functies continu: $\underset{x\rightarrow a}{\lim} f(x) = f(a)$. De grafiek loopt dan glad, zonder sprongen.
Door het symbool ∞ (“oneindig”) stelt men een rij getallen voor die willekeurig groot worden. Met dit concept kan men uitspraken doen als:
- $\underset{x \rightarrow \infty}{\lim} f(x) = 1$ voor steeds sterker negatieve invoerwaarden nadert de uitvoer het getal 1)
- $\underset{x \rightarrow 0}{\lim} f(x) = +\infty$ (voor invoerwaarden steeds dichter bij nul is de uitvoer willekeurig groot)
