Een rationele functie kan worden geschreven als het quotiënt van veeltermen:
$$f(x) = \frac{A_0 + A_1x + A_2x^2 + …. + A_nx^n}{B_0 + B_1x + B_2x^2 + … + B_mx^m}.$$
Dergelijke functies hebben asymptotisch gedrag
- verticale asymptoten of “gaten” bij nulpunten van de noemer
- een horizontale asymptoot als n ≤ m
- een schuine asymptoot als n = m + 1.
Om de horizontale of schuine asymptoot te bepalen voert men een (gedeeltelijke) staartdeling uit (zie paragraaf 34.3).
Bepaal de horizontale of schuine asymptoot van $f(x) = \frac{2x^3 – 5x^2 + 3}{x^2 + 4x – 10}.$
Deling geeft:
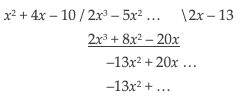
Dus is de lijn y = 2x – 13 een schuine asymptoot.
