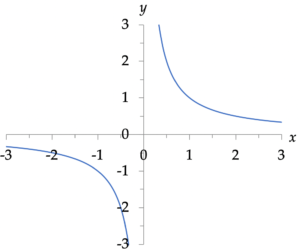
De eenvoudigste rationele functie is
$$f(x) = \frac{1}{x}.$$
Het domein bestaat uit alle reële getallen behalve nul, om deling door nul te voorkomen. De grafiek is een orthogonale hyperbool, met een horizontale en een verticale asymptoot. (In dit geval, de lijnen y = 0 en x = 0.)
De afgeleide $f'(x) = \frac{-1}{x^2}$ is altijd negatief: de grafiek daalt overal. Er zijn geen buigpunten, maar in het gat in het domein, x = 0, verspringt de grafiek van “bol” naar “hol”.
Alle functies van de vorm
$$f(x) = \frac{Ax + B}{Cx + D}$$
hebben soortgelijk gedrag; hun grafiek is simpelweg een translatie (verschuiving) van f(x) = 1/x.
$f(x) = \frac{2x + 1}{x+1} = 2 – \frac{1}{x+1}$ $f(x) = \frac{2x-5}{x-3} = 2 + \frac{1}{x-3}$>
asymptoten: x = –1, y = 2 asymptoten: x = 3, y = 2
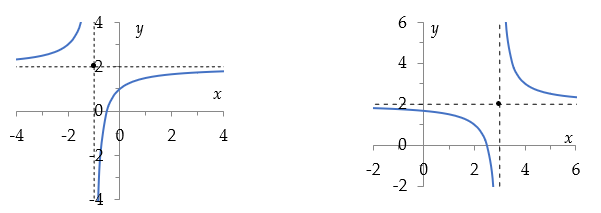
Bepaal de asymptoten van $f(x) = \frac{-x + 10}{3x + 7}.$
- Het domein heeft een gat waar de noemer nul zou zijn: $3x + 7 = 0$, ofwel $X = – 2 \frac{1}{3}$. Dit is de ligging van de verticale asymptoot.
- Voor zeer grote of zeer kleine waarden van x “wint” x het van de getallen 10 en 7:
$$ \lim_{x \rightarrow \pm \infty}\frac{-x + 10}{3x + 7} = \lim_{x \rightarrow \pm \infty}\frac{-x}{3x} = – \frac{1}{3} $$
Dus is de lijn $y = -\frac{1}{3}$ de horizontale asymptoot.
