De eenvoudigste groep irrationele functies zijn die met een vierkantswortel, waaronder een lineaire of kwadratische uitdrukking staat. De grafiek van een dergelijke functie is een halve kegelsnede. Een aantal karakteristieke voorbeelden:
$f(x) = \sqrt{x}$ $f(x) = -\frac{1}{2}\sqrt{4x^2 + 5} + 3$
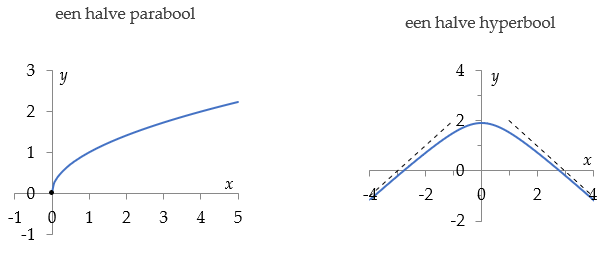
$f(x) = \sqrt{9-x^2}$ $f(x) = \sqrt{x^2 + x – 2}$
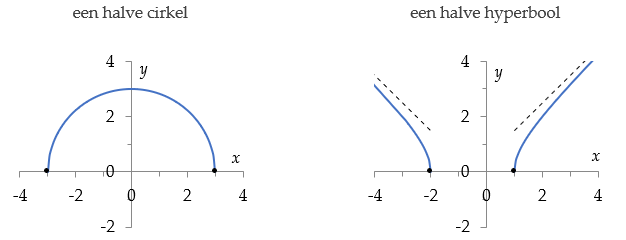
Het domein is meestal begrensd omdat men niet de wortel van een negatief getal mag trekken. Aan de rand van het domein is de raaklijn aan de grafiek verticaal; de eerste afgeleide wordt daar oneindig groot.
Om de nulpunten te vinden (of andere vergelijkingen van de vorm f(x) = c op te lossen), doet men het volgende:
- isoleer de uitdrukking met de wortel aan één kant van de vergelijking
- neem het kwadraat aan beide zijden
- los op
- controleer of de gevonden oplossingen daadwerkelijk oplossingen zijn; dit is belangrijk omdat het kwadrateren in de tweede stap “extra” oplossingen kan invoeren.
Bepaal het domein en de nulpunten van $f(x) = 6 – 3 \cdot \sqrt{x^2 -4x -1}$
Domein: de uitdrukking onder het wortel teken moet ≥ 0 zijn. Bepaal de randen van dit domein:
$x^2 – 4x – 1 = 0$
$(x-2)^2 = 5$
$x = 2 \pm \sqrt{5}$.
Tussen deze waarden in is $x^2 – 4x -1$ negatief (probeer bijv. x = 2), maar daarbuiten positief. Het domein wordt dus beschreven als
$x \leq 2 – \sqrt{5}$ of $x \geq 2 + \sqrt{5}$.
- Nulpunten: $6-3 \cdot \sqrt{x^2 – 4x – 1} = 0$
$\sqrt{x^2 – 4x + 1 } = 2$ 3√… bijgeteld, door 3 gedeeld
$x^2 – 4x – 1 = 4$ beide zijden gekwadrateerd
$x = -1 \; \text{of} \; x = 5$$ kwadratische vergelijking opgelost
Inderdaad is f(1) = 0 en f(5) = 0.
