Een exponentiële functie heeft voorschrift
$$f(x) = A \cdot B^x$$
met positieve coëfficiënt A en positief grondtal B. Men onderscheidt:
- exponentiële toename / groei: B > 1
- exponentiële afname: B < 1
Het domein bestaat uit alle reële getallen. De functie levert slechts positieve uitvoer.
$\;\;\;\;\;\;\;\;f(x) = 2^x$ $f(x) = (\frac{1}{2})^x$
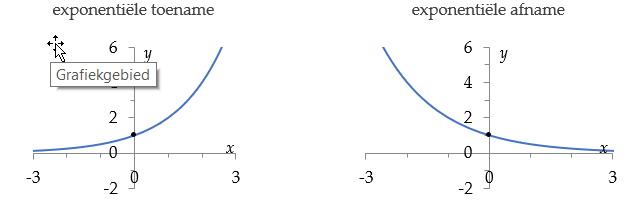
De functie heeft een éénzijdige horizontale asymptoot y = 0, die links zit bij toename en rechts bij afname. De grafiek loopt overal hol en heeft geen buigpunten.
Bij het oplossingen van vergelijkingen$f(x) = c$ heeft men logaritmen nodig. Dergelijke vergelijkingen hebben één oplossing.
Als $f(x) = 5 \cdot 3^{0,7\cdot x}$ , los op f(x) = 50.
$e^{0,7\cdot x} = 10$
$0,7 \cdot x = \ln{10} \approx 2,30$
$x \approx 3,29$
De afgeleide van de exponentiële functie is als volgt:
$$f(x) = A \cdot B^x \Rightarrow f'(x) = A \cdot \ln{B} \cdot B6x = \ln{B} \cdot f(x)$$ $$f(x) = A \cdot e^{Kx} \Rightarrow f'(x) = A \cdot K \cdot e^{Kx} = K \cdot f(x)$$
De afgeleide is dus direct evenredig aan de functie zelf. Dit is typerend voor exponentieel gedrag.
