Een logaritmische functie heeft voorschrift $$f(x) = A \cdot ^B\log{x} $$
met positieve coëfficiënt A en grondtal B (meestal > 1).
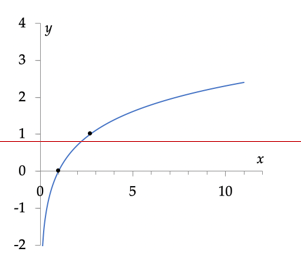
Het domein bestaat uit alle positieve getallen. Aan de rand van het domein geldt $$\lim_{x\downarrow 10} f(x) = \lim_{x \downarrow 10} ^B\log{x} = – \infty$$
dus is de lijn x = 0 een verticale asymptoot.
De grafiek lijkt veel op die van f(x) = ln x (hiernaast). Het nulpunt ligt in x = 1. De grafiek is overal stijgend en loopt bol.
Bepaal het hellinggetal van de raaklijn aan $f(x) = \frac{1}{2} \log{x}$ in het punt (100,1).
- De afgeleide functie is $f'(x) = \frac{1}{2 \ln{10}} \cdot \frac{1}{x}$
- Het hellinggetal (ri.co.) bij x = 100 is dus $\frac{1}{2 \ln{10}} \cdot \frac{1}{199} \approx 0,00217$.
