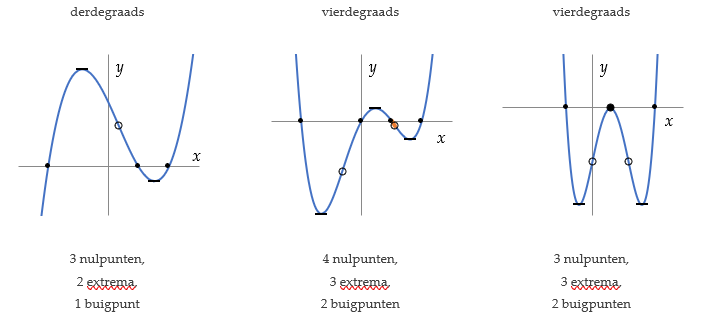
De graad n van de veelterm bepaalt hoeveel “bijzonder gedrag” de functie kan hebben.
- Het aantal nulpunten is ten hoogste n.
- Het aantal extrema (minima, maxima) is ten hoogste n – 1.
- Het aantal buigpunten is ten hoogste n – 2.
De grafiek laat een paar typische voorbeelden zien.
Wanneer de waarde van x zeer groot of zeer klein wordt, “wint” de hoogste macht altijd. In de limiet zal een veeltermfunctie dus veel lijken op de machtsfunctie y = Anxn.
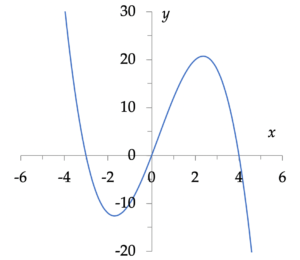
Onderzoek $f(x) = -x^3 + x^2 + 12x$
Dit is een veeltermfunctie van graad drie. Het domein bestaat uit alle reële getallen.
In de limiet zal f(x) lijken op y = –x3. Voor zeer kleine x is f(x) positief, voor zeer grote x is f(x) negatief.
Er zijn ten hoogste drie nulpunten, twee extrema, en één buigpunt.
Berekening van de nulpunten:
$-x^3 + x^2 + 12x = 0$
$-x \cdot (x^2 – x – 12) = 0 \;\;\;\ (\text{-x uitgedeeld})$
$x=0 \;\text{of}\; x^2 – x – 12 = 0$
$x = 0 \; \text{of} \;(x+3)(x-4) = 0 \;\;\;\ (\text{ontbonden in factoren})$
$x = 0 \;\text{of}\; x = -3 \;\text{of}\; x = 4$
Tekenverloop: we weten al dat het tekenverloop begint met + en eindigt met –. Vul bijv. x = –1 en x = +1 voor het gedrag tussen de nulpunten.
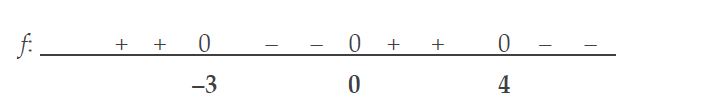
$-3x^2 + 2x + 12 = 0 \;\;\; f'(x) = 0$
$x = \frac{-2 \pm \sqrt{148}}{-6}$
$x \approx -1,70 \text{of} 2,36$
Tussen deze waarden is positief (bijv. f’(0) = 12), daarbuiten negatief. Dus is er een minimum f(–1,70) ≈ –12,6 en een maximum f(2,36) ≈ 20,7.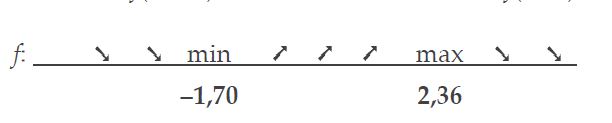
Deze is nul als x = 1/3.
Vóór x = 1/3 is f’ positief en loopt de grafiek hol; na het buigpunt x = 1/3 is de grafiek bol.Voor het buigpunt geldt
- $f(\frac{1}{3}) = 4 \frac{2}{27}$
- $f’\frac{1}{3} = 12\frac{1}{3}$
Dus weten we dat in het buigpunt $(\frac{1}{3},4\frac{2}{27})$ de grafiek het steilst loopt, met ri.co. $12\frac{1}{3}$.
.
