
Een permutatie is een bepaalde ordening van een gegeven aantal voorwerpen. Zo zijn er zes permutaties van de letters A, B, C.
Het aantal permutaties van n voorwerpen is
$$\text{permu}(n) = n \cdot (n-1) \cdot … \cdot 3 \cdot 2 \cdot 1 = n!$$
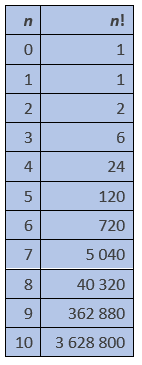
De notatie n! wordt gelezen als “n faculteit”.
Als men acht boeken in willekeurige volgorde op een plank zet, wat is dan de kans dat ze toevallig in alfabetische volgorde staan?
Het aantal mogelijke uitkomsten (hier: permutaties) is
$\text{permu}(8) = 8! = 8 \cdot 7 \cdot … \cdot 2 \cdot 1 = 40320$
Slechts één hiervan is in alfabetische volgorde. Dus geldt:
$P(\text{alfabetisch}) = \frac{1}{40320} \approx 0,0025%$
