Als een lading q wordt beïnvloed door twee of meer andere ladingen, moet men de resultante kracht bepalen. Deze is in principe gelijk aan de som van de afzonderlijke aantrekkingen en afstotingen; hierbij moet men echter rekening houden met de verschillende richtingen. In andere woorden, de krachten moeten vectoriëel worden opgeteld. Wij illustreren dit aan de hand van drie voorbeelden.
Een positieve lading +q geplaatst is op de as van een dipool, bestaande uit twee even grote, tegengestelde ladingen (+Q en –Q):

Lading +Q oefent een afstotende kracht uit op q, ofwel naar links. Anderzijds levert –Q een aantrekkende kracht op q, ofwel naar rechts. Dit tekenen we in een krachtendiagram.

Volgens de wet van Coulomb is elk van de krachten evenredig met Q/d2. In dit geval zijn de ladingen even sterk. Maar omdat de positieve pool +Q dichter bij q ligt dan de negatieve pool –Q, oefent deze een grotere kracht uit: F+ > F–. In het krachtendiagram hierboven is dit aangegeven middels de lengte van de pijlen.
Door hun tegengestelde richtingen heffen F+ en F– elkaar grotendeels op. Echter, omdat F+ sterker is is het totaal niet precies gelijk aan nul, maar een relatief zwakke kracht naar links.

Nu beschouwen we een situatie met lading q op de middelloodlijn van een dipool:
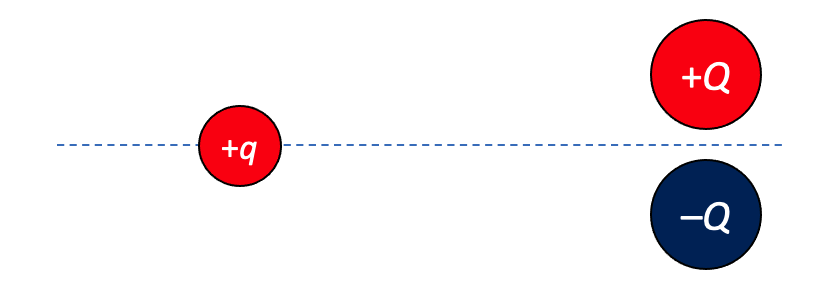
Opnieuw zijn zowel afstoting als aantrekking in het spel. De richtingen zijn nu diagonaal. De afstanden zijn gelijk, zodat beide krachten even sterk zijn.
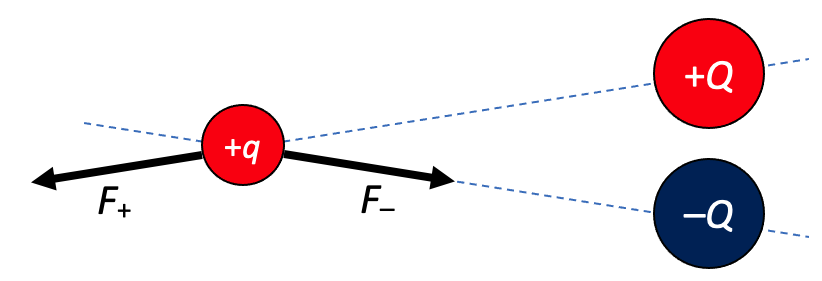
De resultante kracht is nu minder gemakkelijk te bepalen, omdat de krachten niet op één lijn liggen. Er zijn verschillende technieken beschikbaar.
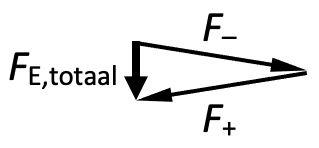
(a) Grafisch: Plaats de pijlen, met juiste lengtes en richtingen, kop-aan-staart. Verbind de staart van de eerste pijl met de kop van de laatste pijl: dit is de vectoriële som.
(b) Redenering met componenten: De horizontale componenten van F+ en F– zijn precies even sterk in tegengestelde richtingen. Ze heffen elkaar dus op; de resultante kracht heeft geen horizontale component. De verticale componenten zijn veel zwakker, maar beide zijn naar onder gericht. Optellen lever dus een relatief zwakke verticale component die omlaag gericht is.
Beide methoden leiden tot de conclusie dat de kracht op q in dit geval relatief zwak is en omlaag gericht.

Tenslotte berekenen we de resultante kracht op lading q in de volgende situatie:

Lading Q1 produceert een afstotende kracht (omhoog); Q2, een aantrekkende kracht (naar links).
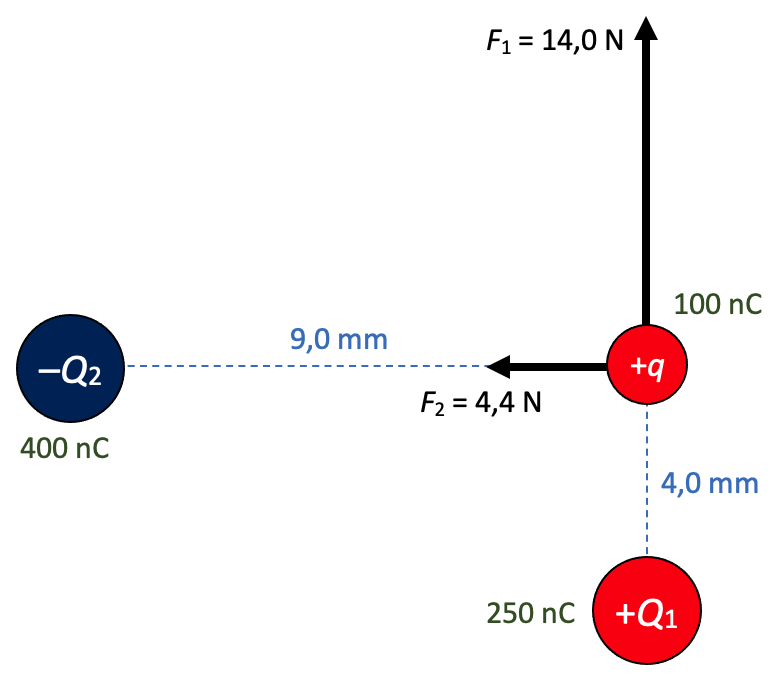
In dit geval hebben we genoeg informatie om de krachten F1 en F2 nauwkeurig te berekenen:
$$F_1 = k \frac{Q_1 q}{d^2} = 8{,}99 \cdot 10^9 \cdot \frac{(250 \cdot 10^{-9}) \cdot (100 \cdot 10^{-9})}{\left(4,0 \cdot 10^{-3}\right)^2} = 14 \; \text{N};$$
$$F_2 = k \frac{Q_2 q}{d^2} = 8{,}99 \cdot 10^9 \cdot \frac{(400\cdot 10^{-9}) \cdot (100 \cdot 10^{-9})}{\left(9,0 \cdot 10^{-3}\right)^2} = 4{,}4 \; \text{N}.$$
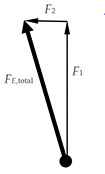
Voor de resultante kracht op q tellen we F1 en F2 vectorieel op. Omdat de krachten loodrecht op elkaar staan, kan men hiervoor de stelling van Pythagoras gebruiken.
$$F_{E,\text{totaal}} = \sqrt{14^2 + 4{,}4^2} = 15 \; \text{N}.$$
