De verhoudingen tussen de zijden zijn volledig bepaald door α. Dus spreken we over de goniometrische verhoudingen die behoren bij de hoek.
- De sinus van α is de verhouding tussen overstaande en schuine zijde.
- De cosinus van α is de verhouding tussen aanliggende en schuine zijde.
- De tangens van α is de verhouding tussen overstaande en aanliggende zijde.
$$\sin{\alpha} = \mathrm{\frac{overstaand}{schuin}; \;\;\; \cos {\alpha} = \frac{aanliggend}{schuin}; \;\;\; \tan{\alpha} = \frac{overstaand}{aanliggend}}.$$
ezelsbruggetje: SOS CAS TOA.
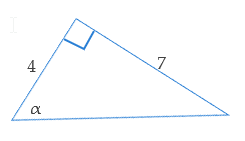
Bepaal cos α in de hier getoonde driehoek.
De cosinus is de verhouding tussen aanliggende en schuine zijde. De aanliggende zijde heeft lengte 4. Voor de schuine zijde gebruiken we de stelling van Pythagoras:
$\mathrm{schuin = \sqrt{4^2 + 7^2} = \sqrt{65}}$
$\cos{\alpha} = \mathrm{\frac{aanliggend}{schuin} = \frac{4}{\sqrt{65}}}$
Een rechthoekige driehoek heeft een hoek van 10˚ en de kortste zijde is 8,0 cm. Bepaal de andere zijden.
De kortste zijde ligt tegenover de kleinste hoek; het is dus de overstaande zijde. Daarom geldt:
$\mathrm{\tan = 8,0 ; cm / aanliggend \Rightarrow aanliggend = 8,0 / \tan{10^\circ} = 45,4 \; cm}$
$\mathrm{\sin = 8,0 \; / schuin \Rightarrow schuin = 8,0 / \sin{10^\circ} = 46,1 \; cm}$
$ (\mathrm{of: \; schuin = \sqrt{8,0^2 + 45,4^2} = 46,1 \; cm}).$
