- standaardoplossing: $x_1 = arc \sin c$ (tussen –90˚ en +90˚)
- spiegelbeeld: $x_2 = 180^\circ – x_1 \;\;\; \text{of} \;\;\; \pi – x_1$
- verdere oplossingen: x1 ± veelvouden van 360˚; x2 ± veelvouden van 360˚
- standaardoplossing: $x_1 = arc \cos c$ (tussen 0˚ en 180˚)
- spiegelbeeld: $x_2 = -x_1$
- verdere oplossingen: x1 ± veelvouden van 360˚; x2 ± veelvouden van 360˚
- standaardoplossing: $x_1 = arc \tan c$ (tussen –90˚ en +90˚)
- verdere oplossingen: x1 ± veelvouden van 180˚;
Bepaal alle oplossingen van $2 \cdot \sin{(3x + 15^\circ)} = -\sqrt{3}$ met x tussen 0˚ en 360˚.
- Deel de vergelijking door 2: $\sin{(3x + 15^\circ)} = – \frac{1}{2}$.
- We weten dat $\sin {60^\circ} = \frac{1}{2}\sqrt{3}$ . Hier hebben we te maken met het spiegelbeeld in kwadrant IV: dus $arc \sin{\frac{1}{2}\sqrt{3}-60^\circ}$ (standaardoplossing).
- De spiegelbeeldoplossing is 180˚ – (–60˚) = 240˚.
- Dus hebben we $3x + 15^\circ = -60 ^\circ \;\;\;\text{of} \;\;\; 240^\circ \;\;\; \pm \text{veelvouden van} 360^\circ$
- Als x tussen 0˚ en 360˚ ligt, dan ligt 3x + 15˚ tussen 15˚ en 1095˚:
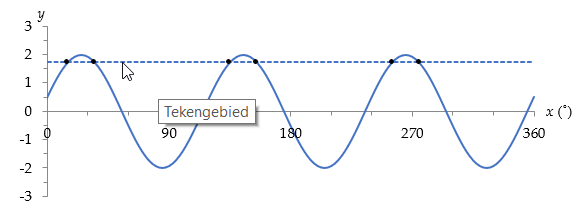
- De functie staat hieronder getekend met de oplossingen.
- Als x tussen 0˚ en 360˚ ligt, dan ligt 3x + 15˚ tussen 15˚ en 1095˚:
$$3x + 15^\circ = 300^\circ, 660^\circ, 1020^\circ,\;\;\; 240^\circ, 600^\circ, 960^\circ$$ $$x = 95^\circ, 215^\circ, 335^\circ, \;\;\; 75^\circ, 195^\circ, 315^\circ.$$
- De functie $2 \cdot \sin{(3x + 15^\circ)}$ staat hieronder getekend met de oplossingen.