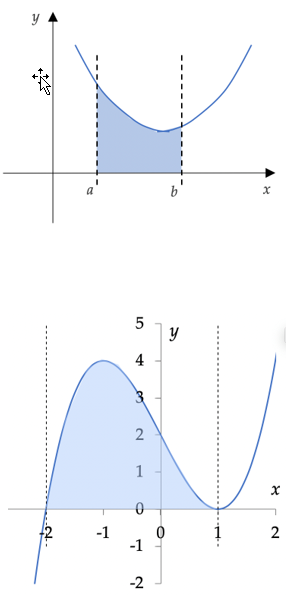
De bepaalde integraal $\int_a^b f(x) dx$ is gelijk aan een oppervlakte onder de grafiek van f. Het gaat om het gebied ingesloten door:
- de grafiek van f
- de x-as
- de verticale lijn y = a
- de verticale lijn y = b.
Ligt die gebied onder de x-as, dan telt dit als negatieve oppervlakte.
Dit is de grafiek van de functie
$f(x) = x^3 – 3x + 2$
Bepaal de oppervlakte van het aangegeven gebied.
Eerst controleren wij dat x = –2 en x = 1 inderdaad de nulpunten zijn. Zij vormen de grenzen van de integraal.
De primitieve is $\int f(x) dx = \frac{1}{4}x^4 – 1 \frac{1}{2}x^2 + 2x + C$.
De bepaalde integraal is
$\int_{-2}^{1} (x^3 – 3x + 2 dx = [\frac{1}{4}x^4 – 1 \frac{1}{2}x^2 + 2x]_{-2}^{1}$
$= (\frac{1}{4} \cdot 1^4 – 1 \frac{1}{2} \cdot 1^2 + 2 \cdot 1) – (\frac{1}{4} \cdot (-2)^4 – 1 \frac{1}{2} \cdot (-2)^2 + 2 \cdot (-2))$.
$=(\frac{1}{4} – 1 \frac{1}{2} + 2) – ( 4 – 6 – 4) = \frac{3}{4} – (-6) = \frac{27}{4}$
Dit is dus de oppervlakte onder de grafiek.
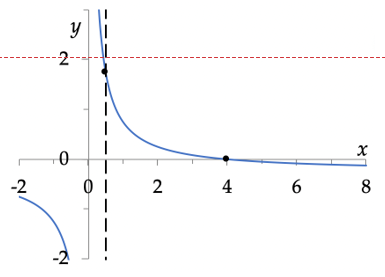
Bereken de oppervlakte ingesloten door de grafiek van
$f(x) = \frac{1}{x} – \frac{1}{4}$
de x-as, en de verticale lijn x = 1.
Eerst tekenen we de grafiek.
De gegeven functie snijdt de x-as in x = 4; dat is dus de rechtergrens van de integratie.
De primitieve is
$\int (\frac{1}{x} – \frac{1}{4})dx = \ln |x| – \frac{1}{4}x + C$ Gebruik dit nu voor de bepaalde integraal:
$\int (\frac{1}{x} – \frac{1}{4})dx = \left [ \ln |x| – \frac{1}{4}x\right ]_1^4 = (\ln 4 – \frac{1}{4}\cdot 4) – (\ln 1 – \frac{1}{4} \cdot 1)$
$=(\ln 4 – 1) – 0 – \frac{1}{4} = \ln 4 – \frac{3}{4} \approx 0,636.$
Als de grafiek onder de x-as loopt, vindt men de oppervlakte als een negatief getal. Integreert men over een interval waarbij de grafiek zowel boven als onder de x-as loopt, dan heffen deze “negatieve” bijdragen de positieve bijdragen op.
Als gevraagd wordt de oppervlakte te bepalen tussen de grafieken van twee functies f(x) en g(x), integreer dan het verschil: $\mathrm{opp} = \int(f(x) – g(x))dx.$
