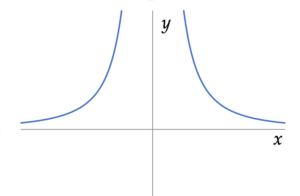
Rationele functies van hogere graad kunnen allerlei gedrag vertonen. Zelfs een relatief eenvoudig geval als #f(x) = \frac{1}{x^2}$ laat hier iets van zien (zie grafiek rechts).
Naast horizontale en verticale asymptoten moet men ook letten op mogelijke “gaten” in de grafiek. Deze ontstaan als de teller en noemer beide nul zijn voor een bepaalde waarde x. Hoewel hier een gat in het domein zit (de deling 0/0 mag niet), kan de grafiek gewoon glad verlopen. De technische term is ophefbare discontinuïteit.
Onderzoek $f(x) = \frac{x^2 + 4x + 4}{-x^2 -3x + 4}$.
- Nulpunten van de noemer:
$$-x^2 – 3x + 4 = 0 \Rightarrow -(x+4) \cdot (x-1) = 0 \Rightarrow x = -4 \; \text{of}\; x = 1.$$
- Op deze plaatsen zit een gat in het domein, met verticale asymptoten.
- De nulpunten van f zijn de nulpunten van de teller:
$$x^2 + 4x + 4 = 0 \Rightarrow (x+2)^2 = 0 \Rightarrow x = -2.$$
- Limietgedrag: voor zeer kleine/grote waarden “winnen” de kwadraattermen, dus
$$\lim_{x \rightarrow \pm \infty} f(x) = \lim_{x \rightarrow \pm \infty}\frac{x^2}{-x^2} = -1.$$
De functie heeft dus een horizontale asymptoot, y = –1.
- De eerste afgeleide wordt gevonden met de quotiëntregel:
$$f'(x) = \frac{(2x+4)(-x^2 – 3x + 4) – (x^2 + 4x + 4)(-2x-3)}{(-x^2 – 3x + 4)^2} = \frac{x^2 + 16x + 28}{(-x^2 -3x + 4)^2}.$$
- Deze is nul als $x^2 + 16x + 28=0$ ofwel x = –14 of –2. Daar vindt men de extrema. Controleer het teken van f’(x) om te zien dat (–14, 0,96) een maximum is en (–2, 0) een minimum.
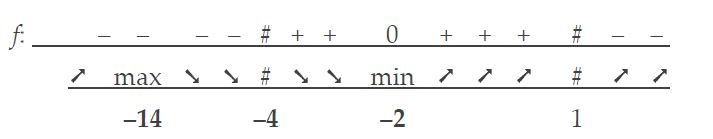
In de grafiek hieronder ziet men dat het maximum bij x = –14 moeilijk te zien is. Het ligt namelijk maar 0,04 boven de horizontale asymptoot. Er moet zich dus ook een buigpunt ter linkerzijde van het maximum bevinden. Berekening van de tweede afgeleide f’’ is echter veel werk; we laten het hier achterwege.

