In een histogram zijn de gegevens al enigszins geordend. Echter, vaak wil men een steekproef (en daarmee, hopelijk, de populatie) karakteriseren middels een enkele getalswaarde, die een soort “gemiddelde” weergeeft. Zo’n getal heet een centrummaat.
Zeker drie centrummaten worden veel gebruikt in de statistiek. Door deze te berekenen voor een (voldoend grote) steekproef, heeft men ook een schatting voor de waarde voor de populatie.
- De modus van een steekproef is de waarde met de hoogste frequentie. Uit bovenstaande grafiek is de modus bijvoorbeeld gelijk is aan 1.
- Om de mediaan van een steekproef te bepalen, ordert men de gegevens van laag naar hoog. Het getal dat midden in de lijst staat is de mediaan. (Als de steekproefgrootte even is, neemt men het gemiddelde van het middelste paar.)

De tabel beschrijft dezelfde steekproef als het histogram hierboven, gesorteerd van laag naar hoog. De middelste twee waarden zijn gearceerd: zij bepalen de mediaan.
$$M = \frac{1}{2} \cdot (1 + 2) = 1\frac{1}{2}$$
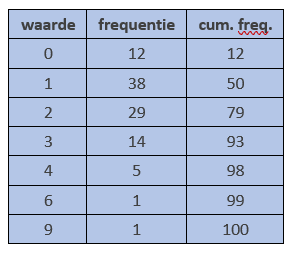
Als men een lijst frequenties heeft, kan men de mediaan gemakkelijker bepalen door de cumulatieve frequentie bij te houden; dat is, de som van frequenties tot en met de gegeven waarde. Zie nevenstaande tabel.
Omdat er 100 elementen zijn, zijn de middelste elementen die met volgnummers 50 en 51. Die zijn nu gemakkelijk te vinden met behulp van de laatste kolom.
- Het gemiddelde wordt berekend als
$$\overline{x}=\frac{\sum{_i}x_i}{n}$$
waarbij n de grootte van de steeproef is. Als de steekproef beschreven wordt als een lijst van verschillende waarden met hun frequenties, dan berekent men:
$$\overline{x}=\frac{\sum{_i}f_ix_i}{\sum{_i}f_i}$$
(De som van frequenties ${\sum{_i}f_i}$ is vanzelfsprekend gelijk aan de steekproefgrootte n.)
Het gemiddelde is de meest gebruikte centrummaat; het is gemakkelijk te berekenen, en is wiskundig goed hanteerbaar. Echter, een groot nadeel is dat uitschieters (opvallend hoge of lage waarden) veel invloed uitoefenen op de ligging van het gemiddelde. Om die redenen is de mediaan vaak een betrouwbaarder centrummaat.
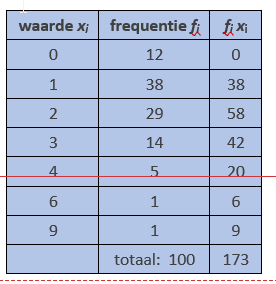
De tabel laat de stappen zien in de berekening van het gemiddelde voor bovenstaande steekproef. Wij vinden
$\overline{x}=\frac{\sum{_i}f_ix_i}{\sum{_i}f_i}=\frac{173}{100} = 1,73$
