Een spreidingsmaat beschrijft in hoeverre de waarden in een steekproef verspreid zijn.
- De min-max afstand is het verschil tussen de hoogste en de laagste waarde in de steekproef.
$$\mathrm{min-max afstand = hoogste waarde – laagste waarde.}$$
- Hoewel deze spreidingsmaat gemakkelijk te berekenen is, is hij nogal onbetrouwbaar. Hij zegt niets over de “gewone” elementen van de steekproef, maar alleen over de meest extreme uitschieters.
- De zgn. kwartielen en decielen worden, net als de mediaan, berekend door de gegevens in een steekproef te sorteren. Vervolgens bepaalt men:
- eerste kwartiel: de waarde op 25% van de lijst
laatste kwartiel: de waarde op 75% van de lijst - eerste deciel: de waarde op 10% van de lijst
laatste deciel: de waarde op 90% van de lijst
- eerste kwartiel: de waarde op 25% van de lijst
- Vervolgens definieert men:
kwartielafstand = laatste kwartiel – eerste kwartiel
decielafstand = laatste deciel – eerste deciel
- Het voordeel van deze spreidingsmaten is dat zij minder gevoelig zijn voor uitschieters. Zij zullen ook beter overeenstemmen met de overeenkomstige waarden voor de populatie.

Opnieuw dezelfde steekproef; de decielen zijn onderstreept en de kwartielen vetgedrukt.
min-maxafstand = 9 – 0 = 9
kwartielafstand = 2 – 1 = 1
decielafstand = 3 – 0 = 3
- De standaarddeviatie (σ) is de meest gebruikte spreidingsmaat in de statistiek. Zij wordt als volgt berekend:
- Voor elk element berekent men het kwadraat van het verschil met het gemiddelde.
- Bereken het gemiddelde van deze kwadratische verschillen; dit heet de variantie.
- De standaarddeviatie is de vierkantswortel van de variantie.
In formulevorm,
$$\text{Var} \; x = \frac{\sum{_i}(x_i – \overline{x})^2}{n} \; \text{of ook } \frac{\sum{_i}f_i (x_i – \overline{x})^2}{\sum{_i}f_i}$$$$\sigma_x = \sqrt{\text{Var }x} = \sqrt{\frac{\sum{_i}f_i (x_i – \overline{x})^2}{n}}$$
De standaarddeviatie van de populatie is op deze wijze gedefinieerd. Zij geeft ruwweg weer hoeveel de waarden gemiddeld afwijken van het populatiegemiddelde.
Men zou deze formule ook kunnen toepassen op een steekproef. Echter, de zo gevonden waarde neigt systematisch iets lager te liggen dan de standaarddeviatie van de populatie. Om hiervoor te corrigeren moet men gebruikmaken van de steekproefdeviatie s:
$$s_x = \sqrt{\frac{\sum{_i}(x_i – \overline{x})^2}{n-1}}$$(Merk op dat de noemer nu n – 1 is in plaats van n.) De steekproefdeviatie is een eerlijke schatter van de standaarddeviatie van een populatie.
Bekijk nog eenmaal de steekproef van de vorige voorbeelden. We bepaalden eerder al dat het gemiddelde 1,73 is.
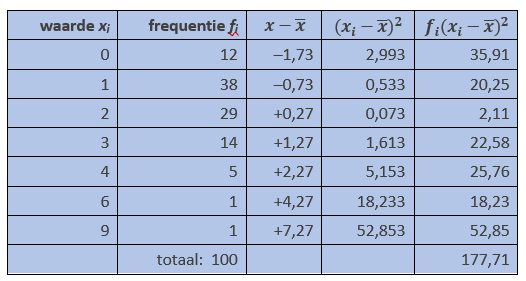
Om de steekproefdeviatie te bepalen delen wij nu door n – 1 = 99, en nemen wij de vierkantswortel:
$$s_x = \sqrt{\frac{\sum{_i}f_i \cdot (x_i – \overline{x})^2}{n-1}} = \sqrt{\frac{177,71}{99}}=1,34$$Op grond van de steekproef concluderen wij omtrent de populatie:
- dat het gemiddelde ongeveer 1,73 is
- dat de waarden “gemiddeld” ongeveer 1,34 afwijken van dat gemiddelde
