Wanneer men combinaties telt, telt men variaties zonder op volgorde te letten. De grepen XYZ en ZXY stellen dus dezelfde combinatie voor.
Het aantal combinaties van k elementen gekozen uit n mogelijkheden zonder herhaling is gelijk aan
$$\text{combi}(n,k) = \frac{\text{vari}(n,k)}{\text{permu}(k)} = \frac{n \cdot (n-1) \cdot … \cdot (n – k +1)}{k \cdot (k-1) \cdot … \cdot 3 \cdot 2 \cdot 1} = \frac{n!}{k! \cdot (n-k)!} = {n \choose k}$$
Deze getallen heten ook wel binomiaalcoëfficiënten. Zij worden geschreven als ${n \choose k}$, uitgesproken als “n boven k”. De zgn. driehoek van Pascal geeft een overzicht van deze getallen.

Op een schaal liggen een appel, een banaan, een kiwi, een mango, een peer, en een sinaasappel. Als men willekeurig drie vruchten hiervan neemt, wat is dan de kans dat dit een banaan, een peer en een sinaasappel zijn?
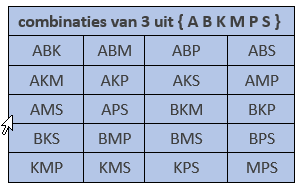
Het aantal combinaties (zonder herhaling, vanzelfsprekend) van drie vruchten uit zes is:
$$\text{combi}(6,3) = {6 \choose 3} = \frac{6 \cdot 5 c\dot 4}{3 \cdot 2 \cdot 1} = 20$$
De kans dat men nu net BPS kiest is dus 1/20 = 5%.
Een stapel met 6 rode en 4 blauwe kaarten wordt geschud. Als ik willekeurig 3 van de deze kaarten pak, hoe groot is de kans dat ze allemaal rood zijn?
Eerst tellen wij hoeveel combinaties van drie kaarten men kan maken met een stapel van 10 kaarten:
$\text{combi}(10,3) = {10 \choose 3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 120.$
Vervolgens tellen wij hoeveel combinaties van drie kaarten men kan maken uit de 6 rode kaarten:
$\text{combi}(6,3)=\frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} = 20$
De kans dat een van de 120 mogelijke combinaties er een is met alleen rode kaarten is dus
$P(\text{drie rood}) = \frac{\text{aantal combinaties van drie rode kaarten}}{\text{aantal combinaties van drie kaarten}} = \frac{20}{120} = 6$
