De grafiek van de normale verdeling is een klokvormige kromme, die wel bekend staat als de Gauss-kromme. Het hoogste punt van de kromme ligt bij het gemiddelde μ; hoever de grafiek verspreid ligt hangt af van σ. Echter, in alle gevallen is de oppervlakte onder de kromme precies gelijk aan één.
Drie normale verdelingen, met μ = 0, maar verschillende σ-waarden.
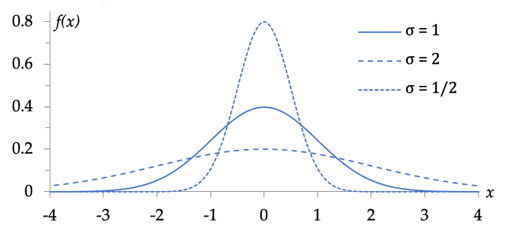
De grafiek heeft twee buigpunten aan weerszijden van het midden. Deze komen overeen met de waarden x = μ – σ en x = μ + σ.
Bepaal het gemiddelde en de standaarddeviatie van onderstaande normale verdeling.
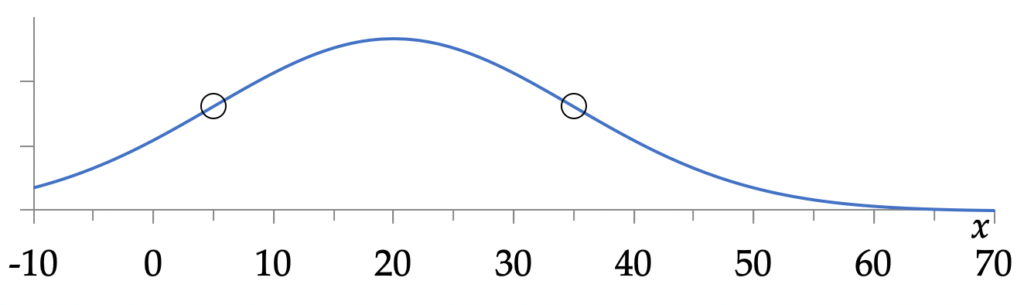
De top van de grafiek ligt op x = 20; de buigpunten op x = 5 en x = 35. Dus is
- gemiddelde = μ = 20
- standaarddeviatie = σ = 20 – 5 = 35 – 20 = 15.
