Stel dat een eigenschap x in een populatie normaal verdeeld is. Men kan zich dan vragen stellen als: Hoe groot is het percentage elementen in de populatie waarvoor x groter is dan een bepaalde waarde? Kleiner is dan een bepaalde waarden? Tussen twee gegeven waarden in ligt? Dit komt op hetzelfde neer als vragen: Hoe groot is de kans dat een willekeurig gekozen element uit de populatie deze eigenschap heeft? In wat volgt zullen wij deze interpretatie als uitgangspunt nemen, en dus de kansnotatie P(…) gebruiken.
Grafisch komen deze percentages/kansen overeen met oppervlaktes onder de grafiek.
Als een bepaalde normale verdeling gegeven is, kunnen we een Z-waarde toewijzen aan elk getal x. Deze beschrijft hoeveel standaarddeviaties x van het gemiddelde ligt:
$$Z=\frac{x-\mu}{\sigma}$$
In plaats van “de kans dat x minstens een halve standaarddeviatie groter is dan het gemiddelde,” kan men nu dus schrijven: $P(Z\geq\frac{1}{2})$
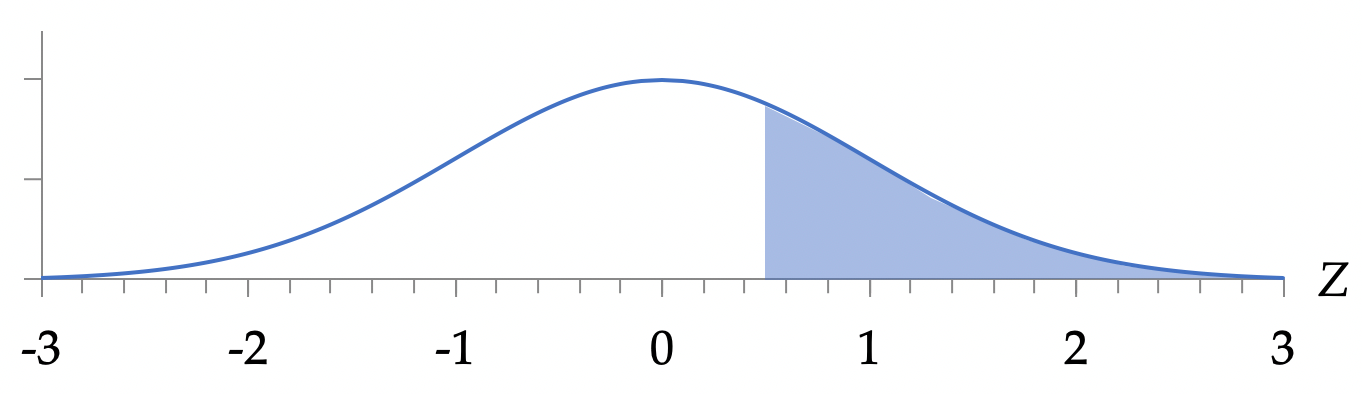
Helaas is er geen formulefunctie om dergelijke kansen uit te rekenen. Wel zijn er tabellen beschikbaar en kunnen rekenmachines en computers de waarden goed benaderen. Aan de hand van de volgende basisfeiten kan men echter ver komen:
- 68% van de waarden liggen binnen één standaarddeviatie van het gemiddelde
- 95% van de waarden liggen binnen twee standaarddeviaties van het gemiddelde
- 99½% van de waarden liggen binnen drie standaarddeviaties van het gemiddelde
(Deze waarden zijn benaderingen.)
In een populatie van vrouwen is de gemiddelde lichaamslengte 165 cm, met een standaarddeviatie van 5 cm. We kiezen willekeurig 200 vrouwen uit deze groep. Hoeveel van deze steekproef zijn er (a) met een lengte tussen 155 en 175 cm? (b) met een lengte onder 160 cm?
We nemen aan de de lichaamslengte normaal verdeeld is.
(a) De Z-waarden die bij 155 cm en 175 cm horen zijn –2 en 2. Uit bovenstaande feiten weten wij dat
$$P(155 < x < 175) = P(-2 < Z < 2) = 0.95;$$het antwoord is dus 95% van de steekproef, ofwel 190 van de 200 vrouwen.
(b) Nu zijn wij op zoek naar een “staartkans”
$$P(x<160) = P(Z<–1)=??$$
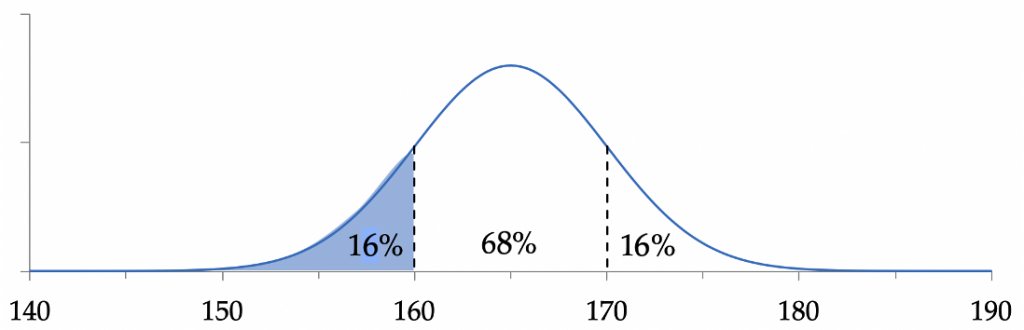
Wij weten dat voor 68% van de vrouwen geldt: –1 < Z < 1. Voor de overige 32% geldt dus óf Z < –1, óf Z > 1. Omdat de normale verdeling symmetrisch is, komt elk van deze mogelijkheden in 16% van de gevallen voor. Het antwoord is dus 16% van de steekproef, ofwel 32 van de 200 vrouwen.
